题目内容
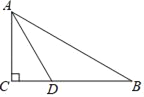
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=2,AC=2![]() .
.
(1)求∠B的度数;
(2)求AB和BC的长.
【答案】(1)30°;(2)![]() .
.
【解析】
(1)根据∠C=90°,CD=2,AC=![]() 得出∠CAD=30°,AD平分∠CAB,即可求出∠B.
得出∠CAD=30°,AD平分∠CAB,即可求出∠B.
(2)由(1)中∠B=30°,利用勾股定理即可求出BC.
解:(1)∵在Rt△ACD中,∠C=90°,CD=2,AC=![]() ,
,
∴tan∠CAD=![]() =
=![]() =
=![]() ,
,
∴∠CAD=30°,
∵AD平分∠CAB,
∴∠CAB=2∠CAD=60°,
∵∠C=90°,
∴∠B=90°﹣60°=30°;
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,
∴AB=2AC=4![]() ,
,
∴BC=![]() =6.
=6.

练习册系列答案
相关题目
【题目】(1)在下列表格中填上相应的值
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | -2 | 3 | 1 | … |

(2)若将上表中的变量![]() 用y来代替(即有
用y来代替(即有![]() ),请以表中的
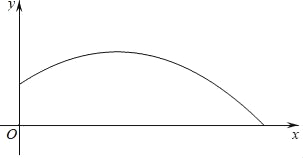
),请以表中的![]() 的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
(3)在(2)的条件下,可将y看作是x的函数 ,请你结合你所画的图像,写出该函数图像的两个性质 :__________________________________________________.
(4)结合图像,借助之前所学的函数知识,直接写出不等式![]() 的解集: ____________
的解集: ____________