Question

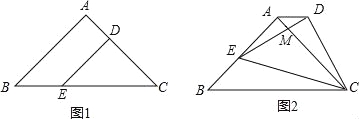
【题目】如图1，在△ABC中，∠BAC=90°，AB=AC=2，D、E两点分别在AC、BC上，且DE∥AB，DC=2，将△CDE绕点C顺时针旋转得到△CD′E′，如图2，点D、E对应点分别为D′、E′、D′、E′与AC相交于点M，当E′刚好落在边AB上时，△AMD′的面积为 ．

Answer 1

【答案】3﹣5．

【解析】

试题分析：如图1，∵∠BAC=90°，AB=AC，∴∠B=∠ACB=45°，∵DE∥AB，

∴∠DEC=∠DCE=45°，∠EDC=90°，∴DE=CD=2，∴CE=CE′=4，

如图2，在Rt△ACE′中，∠E′AC=90°，AC=2，CE′=4，

∴cos∠ACE′=，∴∠ACE′=30°，∴∠D′CA=∠E′CB=15°，

又==，∴△D′CA∽△E′CB，∴∠D′AC=∠B=45°，

∴∠ACB=∠D′AC，∴AD′∥BC，

如图②过点C作CF⊥AD′，垂足为F，∵AD′∥BC，∴CF⊥BC．

∴∠FCD′=∠ACF﹣∠ACD′=30°．

在Rt△ACF中，AF=CF=，∴S△ACF=3，在Rt△D′CF中，CD′=2，∠FCD′=30°，

∴D′F=，∴S△D′CF=．

同理，SRt△AE′C=2，SRt△D′E′C=4，∵∠AME′=∠D′MC，∠E′AM=∠CD′M，

∴△AME′∽△D′MC，∴===

①∴S△AE′M=S△CD′M．②∵S△EMC+S△AE′M=S△AE′C=2，

③S△E′MC+S△CD′M=S△D′EC=4．

由③﹣②，得S△C′DM﹣S△AE′M=4﹣2，

由①，得S△CD′M=8﹣4，

∴S△AD′M=S△ACF﹣S△DCF﹣S△CD′M=3﹣5．

∴△AD′M的面积是3﹣5．

故答案为：3﹣5．