题目内容
【题目】如图，已知∠MON＝120°，点A，B分別在OM，ON上，且OA＝OB＝a，将射线OM绕点O逆时针旋转得到OM′，旋转角为α（0°＜α＜120°，且α≠60°），作点A关于直线OM′的对称点C，画直线BC交OM′于点D，连接AC，AD．
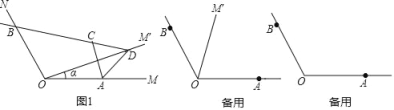
（1）求证：AD＝CD；
（2）如图1，当0°＜α＜60°时，试证明∠ACD的大小是一个定值；
（3）当60°＜α＜120°时，（2）中的结论还成立吗？请补全图形并说明理由；
（4）△ACD面积的最大值为 ．（直接写出结果）
【答案】（1）详见解析；（2）详见解析；（3）结论不变；（4）
a2．
【解析】
（1）证明△ODC≌△ODA（SSS）即可解决问题；
（2）如图1中，由题意OB＝OA＝OC，以O为圆心OC为半径作⊙O，在⊙O上OA的下方取一点H，连接HB，HA．理由圆周角定理，圆内接四边形的性质即可解决问题；
（3）结论不变．如图2中，由题意OB＝OA＝OC，以O为圆心OC为半径作⊙O，理由圆周角定理即可解决问题；
（4）证明△ACD是等边三角形，可知当AC为⊙O的直径时，△ACD的面积最大．
（1）如图1中，连接OC，
∵点A与点C关于直线OD对称，
∴OC＝OA，DC＝DA，
∵OD＝OD，
∴△ODC≌△ODA（SSS），
∴DC＝DA；
（2）如图1中，由题意OB＝OA＝OC，以O为圆心OC为半径作⊙O，在⊙O上OA的下方取一点H，连接HB，HA．
∵∠H＝
∠AOB＝60°，∠H+∠BCA＝180°，
∴∠BCH＝120°，
∴∠ACD＝60°，
∴∠ACD是定值；
（3）结论不变．
理由：如图2中，由题意OB＝OA＝OC，以O为圆心OC为半径作⊙O，
∵∠AOB＝120°，∠ACB＝∠AOB，
∴∠ACB＝60°，
故结论成立；
（4）由（1）（2）可知：DC＝DA，∠ACD＝60°，
∴△ACD是等边三角形，
∴当AC为⊙O的直径时，△ACD的面积最大，
∴S△ADC＝
×（2a）2＝a2．
