题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CP∥AB,在CP上截取CF=CD,连接BF.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,BC=![]() ,求线段CD和BF的长.
,求线段CD和BF的长.

【答案】(1)证明见解析(2)4
【解析】试题分析:(1)连接BD,由AB是直径可得∠BDC=90°,通过证明△BCD≌△BCF,从而得证∠BDC=∠BFC=90°,再根据CP∥AB,从而得∠ABC=90°,即可证明BF是⊙O的切线;
(2)设CD=x,则AD=5-x, 根据勾股定理, ![]() ,即可求得x值,从而求得BD值,再根据全等三角形的对应边相等即可得.
,即可求得x值,从而求得BD值,再根据全等三角形的对应边相等即可得.
试题解析:(1)连接BD,
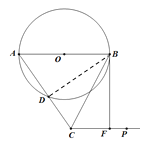
∵ AB是直径,∴∠ADB=90°,∴∠BDC=90°,
∵AB=AC,∴∠ABC =∠ACB,
∵CP∥AB,∴∠ABC =∠BCF,∴ ∠ACB=∠BCF ,
由CF=CD,BC=BC,∴△BCD≌△BCF,∴∠BDC=∠BFC=90°,
∵CP∥AB,∴∠ABC=90°,
∴BF是⊙O的切线;
(2)设CD=x,则AD=5-x,
根据勾股定理, ![]() ,
,
即![]() ,解得x=2,
,解得x=2,
∴CD=2,BD=4 ,
由(1)知△BCD≌△BCF ,∴BD=BF=4.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案【题目】新个税法于2018年1月1日起施行,2018年10月1日起施行最新“起征点:5000元”和税率,《中华共和国个人所得税》中的个人所得税税率如下:
级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过3000元的部分 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
其中“全月应纳税所得额”是指从工资、薪金收入中减去5000元后的金额。(本题只讨论上表内容)
(1)若某一月份扣除税后拿了8000,他交了多少税?
(2)若某一月份纳税额为m元(m>0),他的税前收入是多少?