题目内容
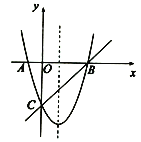
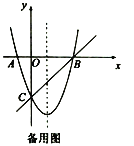
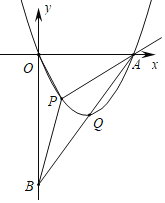
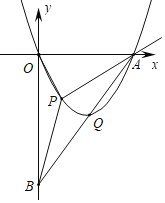
【题目】如图,直线y=2x﹣8分别交x轴、y轴于点A、点B,抛物线y=ax2+bx(a≠0)经过点A,且顶点Q在直线AB上.
(1)求a,b的值.
(2)点P是第四象限内抛物线上的点,连结OP、AP、BP,设点P的横坐标为t,△OAP的面积为s1,△OBP的面积为s2,记s=s1+s2,试求s的最值.
【答案】(1)![]() ;(2)当t=3时,s取得最大值,最大值为18.
;(2)当t=3时,s取得最大值,最大值为18.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标,由二次函数的对称性可得出抛物线的对称轴为直线x=2,利于一次函数图象上点的坐标特征可求出抛物线的顶点Q的坐标,由点A,P的坐标,利用待定系数法即可求出a,b的值;
(2)利用二次函数图象上点的坐标特征可得出点P的坐标,利用三角形的面积公式可找出s1,s2,进而可得出s关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
解:(1)∵直线y=2x﹣8分别交x轴、y轴于点A、点B,
∴点A的坐标为(4,0),点B的坐标为(0,﹣8).
∵抛物线y=ax2+bx(a≠0)经过点A,点O,
∴抛物线的对称轴为直线x=2.
当x=2时,y=2x﹣8=﹣4,
∴抛物线顶点Q的坐标为(2,﹣4).
将A(4,0),Q(2,﹣4)代入y=ax2+bx,得:
![]() ,解得:
,解得:![]() .
.
(2)由(1)得:抛物线解析式为y=x2﹣4x,
∵点P的横坐标为t,
∴点P的坐标为(t,t2﹣4t),
∴s1=![]() ×4×(4t﹣t2)=8t﹣2t2,s2=
×4×(4t﹣t2)=8t﹣2t2,s2=![]() ×8×t=4t,
×8×t=4t,
∴s=s1+s2=﹣2t2+12t=﹣2(t﹣3)2+18.
∵﹣2<0,且0<t<4,
∴当t=3时,s取得最大值,最大值为18.

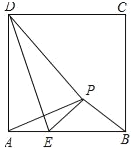
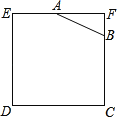
【题目】如图所示,已知边长为4的正方形钢板有一个角锈蚀,其中AF=2,BF=1,为了合理利用这块钢板.将在五边形EABCD内截取一个矩形块MDNP,使点P在AB上,且要求面积最大,求钢板的最大利用率.
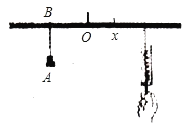
【题目】如图,小华设计了一个探索杠杆平衡的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O的右侧用一个弹簧秤向下拉木杆,改变弹簧秤与点O的距离x(单位:厘米),观察弹簧秤的示数y(单位:牛)的变化情况,实验数据记录如下:
x(单位:厘米) | … | 10 | 15 | 20 | 25 | 30 | … |
y(单位:牛) | … | 30 | 20 | 15 | 12 | 10 | … |
(1)请写出一个符合表格中数据x关于y的函数关系;
(2)当弹簧秤的示数为30牛时,弹簧秤与点O的距离是多少厘米?随着弹簧秤与O点的距离不断减小,弹簧秤的示数将发生怎样的变化?