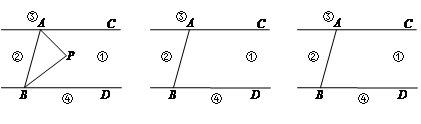题目内容
如图,已知AB∥CD,猜想图1、图2、图3中∠B,∠BED,∠D之间分别有什么关系?请分别用等式表示出它们的关系,并证明.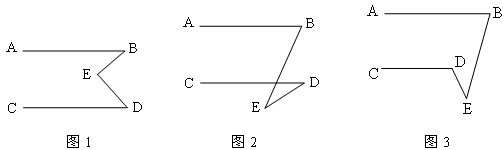

图1:∠B+∠D=∠BED,图2:∠B-∠D=∠BED,∠D=∠B+∠DEB
试题分析:图1:过点E作EF∥AB.运用平行线的性质解答;
图2:根据平行线的性质得∠B=∠BFD,再运用三角形的外角性质解答;
图3:根据平行线的性质得∠B=∠CFE,再运用三角形的外角性质解答.
图1:∠B+∠D=∠BED,图2:∠B-∠D=∠BED,∠D=∠B+∠DEB
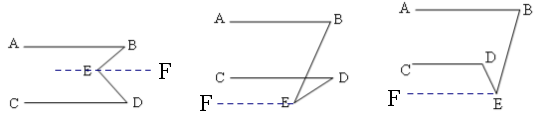
在图1中,有∠BED=∠B+∠D.
证明:过点E作EF∥AB.
∵AB∥CD,
∴EF∥CD.
∴∠B=∠BEF,∠D=∠DEF.
∴∠BED=∠BEF+∠DEF=∠B+∠D.
点评:解题的关键是读懂题意及图形特征,正确作出辅助线,运用平行线的性质及三角形的外角的性质解题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目




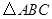 中,
中,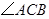 为锐角,点
为锐角,点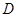 为射线
为射线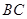 上一点,连接
上一点,连接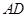 ,以
,以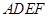 .解答下列问题:
.解答下列问题: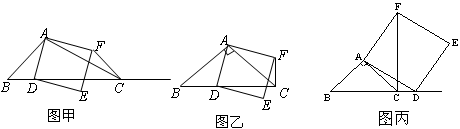
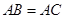 ,
,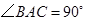 ,
,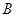 不重合),如图乙,线段
不重合),如图乙,线段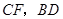 之间的位置关系为 ,数量关系为 .
之间的位置关系为 ,数量关系为 .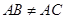 ,
,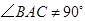 ,点
,点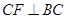 (点
(点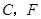 重合除外)?画出图形,并说明理由.(画图不写作法).
重合除外)?画出图形,并说明理由.(画图不写作法).