题目内容
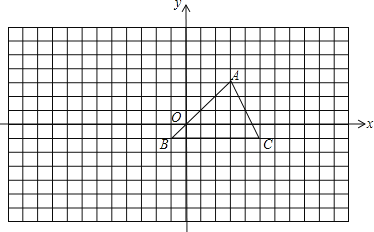
【题目】在△ABC,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点 C 顺时针旋转,旋转角为0 180 ,得到 ABC
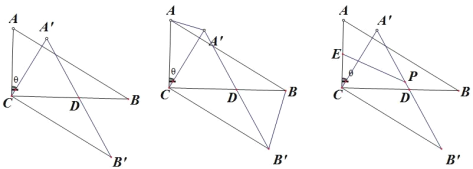
(1)求当角为多少度时, CBD 是等腰三角形;
(2)如图②,连接 AA, BB ,设 ACA , BCB 的面积分别为 S1 , S2 ,求![]() 的值;
的值;
(3)如图③,设 AC 的中点为 E, AB 的中点为 P,AC=a,连接 EP,当旋转角为多少时,EP 长度最大,并求出 EP 的最大值;
【答案】(1)θ=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)分三种情况讨论,由等腰三角形的性质可求解;
(2)通过证明△A'CA∽△B'CB,可得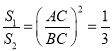 ;
;
(3)由直角三角形的性质可求![]() ,由三角形三边关系可得EC+CP≥EP,即当点P在EC的延长线上时,EP有最大值,由旋转的性质可求旋转角的度数.
,由三角形三边关系可得EC+CP≥EP,即当点P在EC的延长线上时,EP有最大值,由旋转的性质可求旋转角的度数.
解:(1)∵将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
∴∠ABC=∠A'B'C=30°,∠ACA'=∠BCB'=θ,
∵△CB'D是等腰三角形,
①当CD=B'D时,
∴∠BCB'=∠A'B'C=30°=θ
②当CB'=CD时,
∴∠CB'A'=∠CDB'=30°,
∴∠BCB'=120°=θ
③当B'C=B'D,且∠A'B'C=30°,
∴∠B'CD=∠B'DC=75°,
综上所述:当θ=30°或120°或75°时,△CB'D是等腰三角形;
(2)∵∠ACB=90°,∠ABC=30°,
∴tanABC=![]()
∵将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
∴AC=A'C,BC=B'C,∠ACA'=∠BCB',
![]() ,且∠ACA'=∠BCB',
,且∠ACA'=∠BCB',
∴△A'CA∽△B'CB,
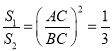 ;
;
(3)如图3,连接CP,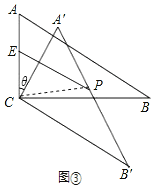
∵∠ACB=90°,∠ABC=30°,AC=a,
∴AB=2a,
∵将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
∴A'B=AB=2a,
∵AC的中点为E,A′B′的中点为P,
∴EC=![]() ,CP=
,CP=![]() A'B=a,
A'B=a,
∵在△ECP中,EC+CP≥EP,
∴当点P在EC的延长线上时,EP有最大值,
∴EP最大值=EC+CP=![]()
∵CP=A'C=A'P=a,
∴∠A'CP=60°,
当点P在EC的延长线上时,θ=∠ACA'=180°-∠A'CP=120°.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案