题目内容
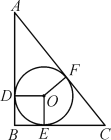
【题目】如图,Rt△ABC的内切圆⊙O与AB,BC,AC分别切于点D,E,F,且AC=13,AB=12,∠ABC=90°,求⊙O的半径长.
【答案】2
【解析】
先利用勾股定理计算出BC=5,再根据切线的性质得OD⊥AB,OE⊥BC,则可判断四边形BEOD为正方形,得到BD=BE=OD,设⊙O的半径为r,则BE=BD=r,AD=AB-BD=12-r,CE=BC-BE=5-r,然后利用切线长定理得到AF=AD=12-r,CF=CE=5-r,于是12-r+5-r=13,再解关于r的方程即可.
解:在Rt△ABC中,∵AC=13,AB=12,
![]()
∵Rt△ABC的内切圆⊙O与AB、BC分别切于点D、E,
∴OD⊥AB,OE⊥BC,
∵∠ABC=90°,
∴四边形BEOD为正方形,
∴BD=BE=OD,
设⊙O的半径为r,则BE=BD=r,AD=AB-BD=12-r,CE=BC-BE=5-r,
∵Rt△ABC的内切圆⊙O与AB、BC、AC分别切于点D、E、F,
∴AF=AD=12-r,CF=CE=5-r,
∴12-r+5-r=13,
解得r=2,
即⊙O的半径长为2.

练习册系列答案
相关题目