��Ŀ����
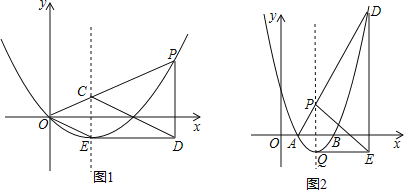
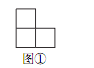
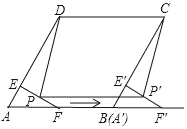
����Ŀ����ͼ�٣���������ABC�У���ACB=90����AC=6��BC=8����DΪ��BC���е㣬����DE��BC��AB�ڵ�E����P�ӵ�D������������DE��ÿ��1����λ���ȵ��ٶ��˶�����PDΪб�ߣ�������DE���Ҳ�������ֱ����DPQ�����P���˶�ʱ��Ϊt���룩��
��1���ú�t�Ĵ���ʽ��ʾ�߶�EP�ij���
��2�����Q���ڱ�AC��ʱt��ֵ��
��3������Q����ABC�ڲ�ʱ������PDQ����ABC�ص�����ͼ�ε����ΪS��ƽ����λ������S��t֮��ĺ�����ϵʽ��

���𰸡���1������P���߶�DE��ʱ��EP =3-t������P��DE���ӳ�����ʱ��EP= t-3����2��t=8s����3��S=
��������
��1������������������ۣ���P���߶�DE�ϣ���P��DE���ӳ����ϣ������߶εĺͲ��ϵ���м��㣻
��2������Q���ڱ�AC��ʱ������Q��QF��DP��F�������ı���CDFQ�Ǿ��Σ���DPQ�ǵ���ֱ�������Σ����DP��2FQ��8�����ɵõ�t��ֵ��
��3������������������ۣ��ٵ���P���߶�DE��ʱ����PDQ����ABC�ص�����Ϊ��DPQ���ڵ���P���߶�DE���ӳ�����ʱ����PDQ����ABC�ص�����Ϊ�ı���EDQG���ֱ����S��t֮��ĺ�����ϵʽ��
�⣺��1������ɵã�DP=t��DE=![]() AC=3��
AC=3��
����P���߶�DE��ʱ��EP=DE-DP=3-t��
����P��DE���ӳ�����ʱ��EP=DP-DE=t-3��
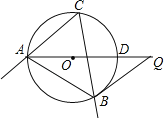
��2����ͼ��ʾ������Q���ڱ�AC��ʱ������Q��QF��DP��F��

�ߡ�C=��CDF=��DFQ=90����
���ı���CDFQ�Ǿ��Σ�
��FQ=CD=![]() BC=4��
BC=4��
�ߡ�DPQ�ǵ���ֱ�������Σ�
��DP=2FQ=8��
��t=![]() =8��s����
=8��s����
��3���ٵ���P���߶�DE��ʱ����PDQ����ABC�ص�����Ϊ��DPQ����DP=t��DP���ϵĸ�Ϊ![]() t��
t��

�ߵ�P�ӵ�D�˶�����E��ʱ��ʱ��Ϊ3s��
�൱0��t��3ʱ��S=![]() ��t��
��t��![]() t=
t=![]() ��
��
�ڵ���P���߶�DE���ӳ�����ʱ����PDQ����ABC�ص�����Ϊ�ı���EDQG��
��ͼ��ʾ����G��GF��PE��F������GFE�ס�BCA����PF=GF��

��AC=6��BC=8��
��EF��FG=3��4��EF��FP=3��4��
��PE=t-3��
��FG=![]() ��t-3����
��t-3����
���PEG�����=![]() ��PE��FG=
��PE��FG=![]() ��
��![]() ��t-3��2��
��t-3��2��
�ɣ�2����֪����Q���ڱ�AC��ʱ��t��ֵΪ8s��
�൱3��t��8ʱ��S=![]() t2-
t2-![]() ��
��![]() ��t-3��2=
��t-3��2=![]() ��
��
����������S��t֮��ĺ�����ϵʽΪ��S= ��
��