题目内容
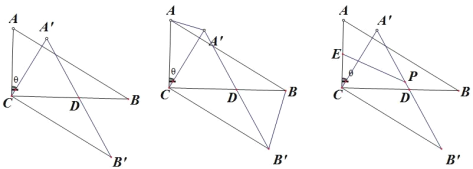
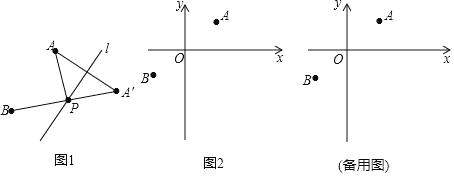
【题目】定义:如图1,A,B为直线l同侧的两点,过点A作直线l的对称点A′,连接A′B交直线于点P,连接AP,则称点P为点A,B关于直线l的“等角点”.
运用:如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(﹣2,﹣
),B(﹣2,﹣![]() )两点
)两点
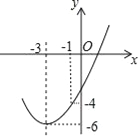
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() ),哪个点是点A,B关于直线x=4的“等角点”;
),哪个点是点A,B关于直线x=4的“等角点”;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的“等角点”,其中m>2,∠APB=α,求证:tan![]() .
.
【答案】(1)点C;(2)见解析
【解析】
(1)点B关于直线x=4的对称点为B′(10,![]() ),由待定系数法求出直线AB′的解析式为y=﹣
),由待定系数法求出直线AB′的解析式为y=﹣![]() x+
x+![]() ,当x=4时,y=
,当x=4时,y=![]() ,即可得出结果;
,即可得出结果;
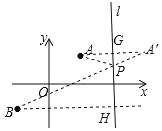
(2)过点A作直线l的对称点A′,连接A′B,交直线l于点P,作BH⊥l于点H,由点A和A′关于直线l对称,得出∠APG=∠A′PG,证明△AGP∽△BHP,得出![]() =
=![]() ,求出m=
,求出m=![]() ,由∠APB=α,AP=A′P,得出∠A=∠A′=
,由∠APB=α,AP=A′P,得出∠A=∠A′=![]() ,在Rt△AGP中,tan
,在Rt△AGP中,tan![]() =
=![]() =
=![]() =
=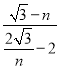 =
=![]() .
.
(1)解:点B关于直线x=4的对称点为B′(10,﹣![]() ),
),
设直线AB′的解析式为:y=kx+b,
则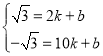 ,
,
解得: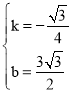 ,
,
∴直线AB′的解析式为:y=﹣![]() x+
x+![]() ,
,
当x=4时,y=![]() ,
,
∴点C(4,![]() )是点A,B关于直线x=4的“等角点”;
)是点A,B关于直线x=4的“等角点”;
(
∵点A和A′关于直线l对称,
∴∠APG=∠A′PG,
∵∠BPH=∠A′PG,
∴∠APG=∠BPH,
∵∠AGP=∠BHP=90°,
∴△AGP∽△BHP,
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
∴mn=2![]() ,
,
∴m=![]() ,
,
∵∠APB=α,AP=A′P,
∴∠A=∠A′=![]() ,
,
在Rt△AGP中,tan![]() =
=![]() =
=![]() =
=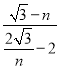 =
=![]() .
.

练习册系列答案
相关题目