题目内容
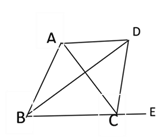
【题目】如图：点E是∠AOB的平分线上一点，ED⊥OA，EC⊥OB，垂足分别为C、D．
求证：（1）OC=OD；
（2）OE是线段CD的垂直平分线．
【答案】见解析
【解析】试题分析：（1）利用角平分线的性质证明Rt△OED≌Rt△OEC，所以OC=OD.
(2)利用（1）的结论，可得OE是CD的垂直平分线.
试题解析：
证明：（1）因为点E是∠AOB的平分线上一点，ED⊥OA，EC⊥OB，
所以ED=EC,
在Rt△OED和Rt△OEC中,
OE=OE，DE=EC，
∴Rt△OED≌Rt△OEC.
∴OC=OD；
（2）∵OC=OD，
∴点O在线段CD的垂直平分线上，
∵DE=DC，
∴点E在线段CD的垂直平分线上，
∴OE是线段CD的垂直平分线．
练习册系列答案
相关题目
