题目内容
【题目】如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．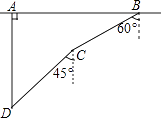
【答案】解：如图，过B作AB的垂线，过C作AB的平行线，两线交于点E；过C作AB的垂线，过D作AB的平行线，两线交于点F，则∠E=∠F=90°，拦截点D处到公路的距离DA=BE+CF．
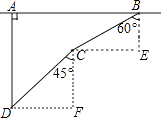
在Rt△BCE中，∵∠E=90°，∠CBE=60°，
∴∠BCE=30°，
∴BE= 
BC= ×1000=500米；
在Rt△CDF中，∵∠F=90°，∠DCF=45°，CD=BC=1000米，
∴CF= 
CD=500 
米，
∴DA=BE+CF=（500+500 ）米，
故拦截点D处到公路的距离是（500+500 ）米．
【解析】根据已知的方向角的度数，可知应添加辅助线， 过B作AB的垂线，过C作AB的平行线，两线交于点E；过C作AB的垂线，过D作AB的平行线，两线交于点F，则∠E=∠F=90°，要求DA的长转化为求BE和CF之和，分别在 Rt△BCE中和Rt△CDF中，利用解直角三角形分别求出BE、CF的长，再求它们的和即可。
【考点精析】通过灵活运用特殊角的三角函数值和解直角三角形，掌握分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)即可以解答此题．
