题目内容
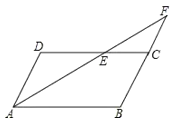
【题目】在△ABC中,AB、AC的垂直平分线分别交BC于D、E,角∠DAE=20°,则∠BAC=___.
【答案】100°
【解析】
根据线段的垂直平分线的性质得到DA=DB,EA=EC,得到∠B=∠DAB和∠C=∠EAC,根据三角形内角和定理计算得到答案.
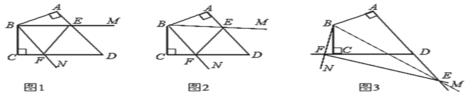
解:第一种情况DM和NE不在三角形内相交
如图:

∵DM是线段AB的垂直平分线,
∴DA=DB,
∴∠B=∠DAB,
同理∠C=∠EAC,
∵∠B+∠DAB+∠C+∠EAC+∠DAE=180°,
∴∠DAB+∠EAC=80°,
∴∠BAC=100°,
第二种情况DM和NE在三角形内相交
如图:

∵DM是线段AB的垂直平分线,
∴DA=DB,
∴∠B=∠DAB,
同理∠C=∠EAC,
∵∠B+∠DAB+∠C+∠EAC-∠DAE=180°,
∴2(∠DAB+∠EAC)-20°=180°,
∴∠DAB+∠EAC=100°
∴∠BAC=∠DAB+∠EAC-∠DAE=80°,
故答案为: 100°或80°

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目