题目内容
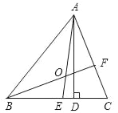
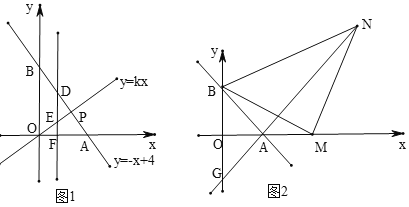
【题目】如图1，已知直线
与坐标轴交于
两点，与直线
交于点
,且点的横坐标是纵坐标的
倍.
(1)求
的值.
(2)
为线段
上一点，
轴于点
，交
于点
,若
，求点坐标.
(3)如图2，
为
点右侧
轴上的一动点，以为直角顶点，
为腰在第一象限内作等腰直角
，连接
并延长交
轴于点
，当点运动时，点的位置是否发生变化?若不变，请求出它的坐标;如果变化，请说明理由.
【答案】(1)
；(2)
；(3)不变，G(0，-4).
【解析】
（1）根据P点的横坐标是纵坐标的3倍，可得k的值；
（2）由图象可知，D、E、F三点在同一条直线上，横坐标相同，可设D、E点横坐标，分别代入解析式可以表示出纵坐标，进而表示出DE、EF的长度，从而构造出方程，求出点D坐标.
（3）过
作
轴于
，根据题目条件，先证明
，进而能够得到AH=NH，得到
为等腰直角三角形，然后得到
也是等腰三角形，进而得到G点的坐标.
解：(1) 
直线
上点P的横坐标是纵坐标的3倍，
若P点纵坐标为a则横坐标为3a，
,
;
(2)设D点横坐标为m,则D点坐标为
，
DF= 
轴于F交
于E，
E点坐标为
EF= 
,
，
，
，
解得：
(3)
点的位置不发生变化，
．
过作轴于，
是等腰直角三角形，
，
，
，
，
，
，
即
，
又
，
，
是等腰直角三角形，
，
，
为等腰直角三角形，
，
∴G(0，-4)．
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题：
（1）完成下表：
姓名 | 平均成绩（分） | 中位数（分） | 众数（分） | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
（2）在这五次测试中，成绩比较稳定的同学是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？
（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．
