题目内容
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.

(1)如图1,若∠1=60°,求∠2=__________;∠3=__________.
(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD. 理由如下:
如图2,过点P作MN∥AB,则∠EPM=∠PEB(__________)
∵AB∥CD(已知) MN∥AB(作图)
∴MN∥CD(__________)
∴∠MPF=∠PFD (__________)
∴__________+__________=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD.请补充完整说理过程(填写理由或数学式)
②当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=__________;
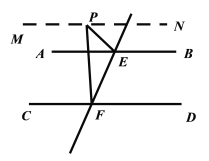
③当点P在图4的位置时,写出∠EPF,∠PEB,∠PFD三个角之间的关系并证明(每一步必须注明理由).
【答案】(1)∠2=60°;∠3=60°;(2)①两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠FPM;②124°;③∠EPF+∠PFD=∠PEB;证明见解析
【解析】
(1)根据对顶角相等求∠2,根据两直线平行,同位角相等求∠3;
(2)①过点P作MN//AB,根据平行线的性质得∠EPM=∠PEB,且有MN//CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB十∠PFD;
②同①;
③利用平行线的性质和三角形的外角性质得到三个角之间的关系.
解:(1)应填∠2=60°,∠3=60°.理由是:
∵∠2=∠1,∠1=60°,
∴∠2=60°,
∵AB//CD
∴∠3=∠1=60°;
(2)①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD. 理由如下:
如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD (两直线平行,内错角相等)
∴ ∠EPM+∠FPM =∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
故答案为:两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠MP
②当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=124°.理由为:
如图3所示,过点P作PM∥AB,
则∠PEB+∠EPM=180°,∠MPF+∠PFD=180°,
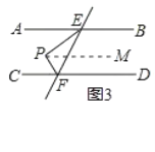
∴∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°,即∠EPF+∠PEB+∠PFD=360°
∴∠PFD=360°-80°-156°=124°;
故答案为:124°
③当点P在图4的位置时,∠EPF,∠PEB,∠PFD三个角之间关系是:
∠EPF+∠PFD=∠PEB
证明如下:
如图4,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
∵AB∥CD(已知),MN∥AB,
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD(两直线平行,内错角相等)
∴∠EPM-∠MPF=∠PEB-∠PFD(等式的性质)
即∠EPF+∠PFD=∠PEB

【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.