题目内容
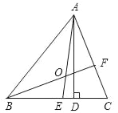
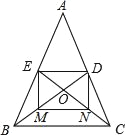
【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.

【答案】(1)证明见解析;(2)四边形DEMN是正方形,证明见解析.
【解析】分析:(1)根据已知条件得到AD=AE,根据全等三角形的性质即可得到结论;
(2)根据三角形中位线的性质得到ED∥BC,ED=![]() BC,MN∥BC,MN=
BC,MN∥BC,MN=![]() BC,等量代换得到ED∥MN,ED=MN,推出四边形EDNM是平行四边形,由(1)知BD=CE,求得DM=EN,得到四边形EDNM是矩形,根据全等三角形的性质得到OB=OC,由三角形的重心的性质得到O到BC的距离=
BC,等量代换得到ED∥MN,ED=MN,推出四边形EDNM是平行四边形,由(1)知BD=CE,求得DM=EN,得到四边形EDNM是矩形,根据全等三角形的性质得到OB=OC,由三角形的重心的性质得到O到BC的距离=![]() BC,根据直角三角形的判定得到BD⊥CE,于是得到结论.
BC,根据直角三角形的判定得到BD⊥CE,于是得到结论.
详解:
(1)解:由题意得,AB=AC,
∵BD,CE分别是两腰上的中线,
∴AD=![]() AC,AE=
AC,AE=![]() AB,
AB,
∴AD=AE,
在△ABD和△ACE中
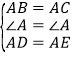 ,
,
∴△ABD≌△ACE(ASA).
∴BD=CE;
(2)四边形DEMN是正方形,
证明:∵E、D分别是AB、AC的中点,
∴AE=![]() AB,AD=
AB,AD=![]() AC,ED是△ABC的中位线,
AC,ED是△ABC的中位线,
∴ED∥BC,ED=![]() BC,
BC,
∵点M、N分别为线段BO和CO中点,
∴OM=BM,ON=CN,MN是△OBC的中位线,
∴MN∥BC,MN=![]() BC,
BC,
∴ED∥MN,ED=MN,
∴四边形EDNM是平行四边形,
由(1)知BD=CE,
又∵OE=ON,OD=OM,OM=BM,ON=CN,
∴DM=EN,
∴四边形EDNM是矩形,
在△BDC与△CEB中,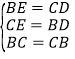 ,
,
∴△BDC≌△CEB,
∴∠BCE=∠CBD,
∴OB=OC,
∵△ABC的重心到顶点A的距离与底边长相等,
∴O到BC的距离=![]() BC,
BC,
∴BD⊥CE,
∴四边形DEMN是正方形.

【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.