��Ŀ����
����Ŀ����֪�ı���ABCD�У���A����C��90�㣬AB��BC����ABC��120�㣬��MBN��60�㣬��MBN��B����ת���������߷ֱ�AD��DC�������ǵ��ӳ��ߣ���E��F��
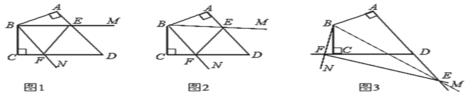
����MBN��B����ת��AE��CFʱ����ͼ1������֤AE+CF��EF��
����MBN��B����ת��AE��CFʱ����ͼ2��ͼ3����������£����������Ƿ�������������������֤���������������߶�AE��CF��EF����������������ϵ����д����IJ��룬����֤����
���𰸡�ͼ2������ͼ�����������½���Ϊ��EF=AE-CF��
��������
������֪��������SAS֤����ABE�ա�CBF���Ӷ��ó���Ӧ����ȣ���Ӧ����ȣ��Ӷ��ó���ABE=��CBF=30������BEFΪ�ȱ������Σ����õȱ������ε����ʼ������֮��Ĺ�ϵ�������Ƴ�AE+CF=EF��ͬ��ͼ2��֤���dz����ģ�ͼ3��������
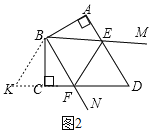
�⣺��AB��AD��BC��CD��AB=BC��AE=CF��
����ABE����CBF��
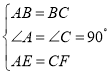 ��
��
���ABE�ա�CBF��SAS����
���ABE=��CBF��BE=BF��
�ߡ�ABC=120������MBN=60����
���ABE=��CBF=30����
��AE=![]() BE��CF=
BE��CF=![]() BF��
BF��
�ߡ�MBN=60����BE=BF��
���BEFΪ�ȱ������Σ�
��AE+CF=![]() BE+
BE+![]() BF=BE=EF��
BF=BE=EF��
ͼ2������ͼ3��������
֤��ͼ2��
�ӳ�DC����K��ʹCK=AE������BK��
����BAE����BCK��
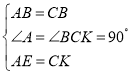 ��
��
����BAE�ա�BCK��
��BE=BK����ABE=��KBC��
�ߡ�FBE=60������ABC=120����
���FBC+��ABE=60����
���FBC+��KBC=60����
���KBF=��FBE=60����
����KBF����EBF��
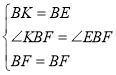 ,
,
���KBF�ա�EBF��
��KF=EF��
��KC+CF=EF��
��AE+CF=EF��
ͼ3���������½���ΪEF=AE-CF��
���ɣ���ͼ3����RT��ABE˳ʱ����ת120����
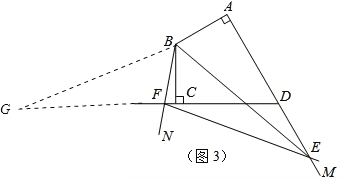
��AB=BC����ABC=120����
��A����C���غϣ���ABE=��CBG��
��BG=BE��FG=CG-CF=AE-CF��
�ߡ�ABC=��ABE+��CBE=120����
���CBG+��CBE=��GBE=120����
�ߡ�MBN=60����
���GBF=60����
����BFG����BFE��
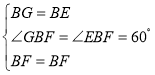 ��
��
���BFG�ա�BFE����SAS��
��GF=EF��
��EF=AE-CF��

 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�