��Ŀ����
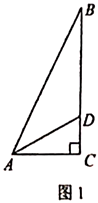
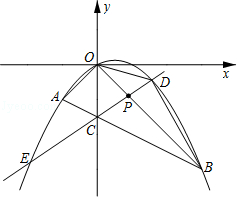
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��m��m������B������Ϊ��n����n���������߾���A��O��B���㣬����OA��OB��AB���߶�AB��y���ڵ�C����֪ʵ��m��n��m��n���ֱ��Ƿ���x2��2x��3=0��������
��1���������ߵĽ���ʽ��
��2������PΪ�߶�OB�ϵ�һ�����㣨�����O��B�غϣ���ֱ��PC�������߽���D��E���㣨��D��y���Ҳࣩ������OD��BD��
�ٵ���OPCΪ����������ʱ�����P�����ꣻ
�����BOD ��������ֵ����д����ʱ��D�����꣮
���𰸡��⣺��1���ⷽ��x2��2x��3=0���� x1=3��x2=��1��
��m��n����m=��1��n=3����A����1����1����B��3����3����
�������߹�ԭ�㣬�������ߵĽ���ʽΪy=ax2+bx��
��![]() ����ã�
����ã�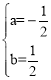 ��
��
�������ߵĽ���ʽΪ![]() ��
��
��2������ֱ��AB�Ľ���ʽΪy=kx+b��
��![]() ����ã�
����ã�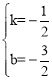 ��
��
��ֱ��AB�Ľ���ʽΪ![]() ��
��
��C��������0��![]() ����
����
��ֱ��OB����O��0��0����B��3����3������ֱ��OB�Ľ���ʽΪy=��x��
�ߡ�OPCΪ���������Σ���OC=OP��OP=PC��OC=PC��
��P��x����x����
��i����OC=OPʱ��![]() �����
�����![]() ����ȥ����
����ȥ����
��P1��![]() ����
����
��ii����OP=PCʱ����P���߶�OC���д����ϣ���P2��![]() ����
����
��iii����OC=PCʱ����![]() �����
�����![]() ����ȥ����
����ȥ����
��P3��![]() ����
����
����������P������ΪP1��![]() ����P2��
����P2��![]() ����P3��
����P3��![]() ����
����
�ڹ���D��DG��x�ᣬ����ΪG����OB��Q����B��BH��x�ᣬ����ΪH��
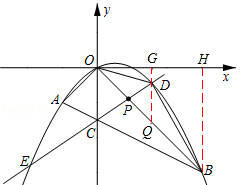
��Q��x����x����D��x��![]() ����
����
S��BOD=S��ODQ+S��BDQ=![]() DQOG+
DQOG+![]() DQGH
DQGH
=![]() DQ��OG+GH��
DQ��OG+GH��
=![]()
=![]() ��
��
��0��x��3���൱![]() ʱ��Sȡ�����ֵΪ
ʱ��Sȡ�����ֵΪ![]() ����ʱD��
����ʱD��![]() ����
����
����������1�����Ƚⷽ�̵ó�A��B��������꣬�Ӷ����ô���ϵ����������κ�������ʽ���ɡ�
��2�����������AB��ֱ�߽���ʽ���Լ�BO����ʽ�������õ��������ε����ʵó���OC=OPʱ����OP=PCʱ����P���߶�OC���д����ϣ���OC=PCʱ�ֱ����x��ֵ���ɡ�
������S��BOD=S��ODQ+S��BDQ�ó�����x�Ķ��κ������Ӷ��ó���ֵ���ɡ�