题目内容
【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.

【答案】8
【解析】
作FG⊥BC于点G,DE’⊥AB于点E’,易证E点和E’点重合,则∠FGD=∠DEP=90°;由∠EDB+∠PDF=90°可知∠EDP+∠GFD=90°,则易得∠EPD=∠GDF,再由PD=DF易证△EPD≌△GDF,则可得FG=DE,故F点的运动轨迹为平行于BC的线段,据此可进行求解.
解:作FG⊥BC于点G,DE’⊥AB于点E’,由BD=4、BE=2与∠B=60°可知DE⊥AB,即∠
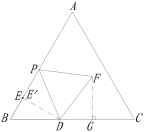
∵DE’⊥AB,∠B=60°,
∴BE’=BD×![]() =2,
=2,
∴E点和E’点重合,
∴∠EDB=30°,
∴∠EDB+∠PDF=90°,
∴∠EDP+∠GFD=90°=∠EDP+∠DPE,
∴∠DPE=∠GFD
∵∠DEP=∠FGD=90°,FD=GP,
∴△EPD≌△GDF,
∴FG=DE,DG=PE,
∴F点运动的路径与G点运动的路径平行,即与BC平行,
由图可知,当P点在E点时,G点与D点重合,
∵DG=PE,
∴F点运动的距离与P点运动的距离相同,
∴F点运动的路径长为:AB-BE=10-2=8,
故答案为:8.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).