Question

【题目】近年来，净水器悄然走进千家万户，某商场从厂家购进了A，B两种型号的净水器，已知A型比B型净水器每台进价多了300元，用7500元购进A型净水器和用6000元购进B型净水器的台数相同．
（1）求每台A型净水器和每台B型净水器的进价分别是多少元？
（2）为了增大B型净水器的销量，商场决定对B型净水器进行降价销售，经市场调查，当每台B型净水器售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台，问将每台B型净水器的定价为多少元时，商家每天销售B型净水器的获得的利润最大？最大为多少？

Answer 1

【答案】
（1）解：设A型净水器每台x元，B型净水器每台y元，根据题意，

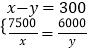得： ，解得： ，

答：每台A型净水器的进价为1500元，每台B型净水器的进价是1200元

（2）解：设每台B型净水器定价为a元时，商家每天销售B型净水器获得的利润为W元，根据题意，

得：W=（a﹣1200）（4+ ）

=﹣ a2+64a﹣48000

=﹣ （a﹣1600）2+3200，

∴当a=1600时，W取得最大值，最大值为3200元；

答：将每台B型净水器的定价为1600元时，商家每天销售B型净水器的获得的利润最大，最大为3200元

【解析】（1）设A型净水器每台x元，B型净水器每台y元，根据：①A型净水器的单价﹣B型净水器的单价=300，②7500元购进A种空气净化器的数量=6000元购进B种空气净化器的数量，列二元一次方程组求解可得；（2）根据：总利润=（每台实际售价﹣每台进价）×销售量，列函数关系式，配方成二次函数的顶点式可得函数的最大值．