题目内容
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. 
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
【答案】
(1)
证明:如图,连接OE.
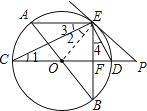
∵CD是圆O的直径,
∴∠CED=90°.
∵OC=OE,
∴∠1=∠2.
又∵∠PED=∠C,即∠PED=∠1,
∴∠PED=∠2,
∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,
∴OE⊥EP,
又∵点E在圆上,
∴PE是⊙O的切线;
(2)
证明:∵AB、CD为⊙O的直径,
∴∠AEB=∠CED=90°,
∴∠3=∠4(同角的余角相等).
又∵∠PED=∠1,
∴∠PED=∠4,
即ED平分∠BEP;
(3)
解:设EF=x,则CF=2x,
∵⊙O的半径为5,
∴OF=2x﹣5,
在RT△OEF中,OE2=OF2+EF2,即52=x2+(2x﹣5)2,
解得x=4,
∴EF=4,
∴BE=2EF=8,CF=2EF=8,
∴DF=CD﹣CF=10﹣8=2,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵AB=10,BE=8,
∴AE=6,
∵∠BEP=∠A,∠EFP=∠AEB=90°,
∴△AEB∽△EFP,
∴![]() ,即
,即![]() ,
,
∴PF=![]() ,
,
∴PD=PF﹣DF=![]() ﹣2=
﹣2=![]() .
.
【解析】(1)如图,连接OE.欲证明PE是⊙O的切线,只需推知OE⊥PE即可;
(2)由圆周角定理得到∠AEB=∠CED=90°,根据“同角的余角相等”推知∠3=∠4,结合已知条件证得结论;
(3)设EF=x,则CF=2x,在RT△OEF中,根据勾股定理得出52=x2+(2x﹣5)2 , 求得EF=4,进而求得BE=8,CF=8,在RT△AEB中,根据勾股定理求得AE=6,然后根据△AEB∽△EFP,得出![]() ,求得PF=
,求得PF=![]() ,即可求得PD的长.
,即可求得PD的长.
此题考查了圆的综合应用,涉及知识点有切线的判定,圆周角定理,勾股定理和相似三角形的性质等.





