题目内容
【题目】如图，抛物线y＝x2在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为A1，A2，A3…An，将抛物线y＝x2沿直线L：y＝x向上平移，得到一系列抛物线，且满足下列条件：①抛物线的顶点M1，M2，M3，…Mn都在直线L：y＝x上；②抛物线依次经过点A1，A2，A3…An，则顶点M2020的坐标为_____．
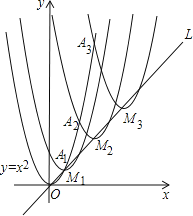
【答案】（4039，4039）
【解析】
根据抛物线的解析式结合整数点的定义，找出点An的坐标为（n，n2），设点Mn的坐标为（a，a），则以点Mn为顶点的抛物线解析式为y=（x-a）2+a，由点An的坐标利用待定系数法，即可求出a值，将其代入点Mn的坐标即可得出结论．
∵抛物线y＝x2在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为A1，A2，A3，…，An，…，
∴点An的坐标为（n，n2）．
设点Mn的坐标为（a，a），则以点Mn为顶点的抛物线解析式为y＝（x﹣a）2+a，
∵点An（n，n2）在抛物线y＝（x﹣a）2+a上，
∴n2＝（n﹣a）2+a，解得：a＝2n﹣1或a＝0（舍去），
∴Mn的坐标为（2n﹣1，2n﹣1），
∴M2020的坐标为（4039，4039）．
故答案为：（4039，4039）．
练习册系列答案
相关题目
