题目内容

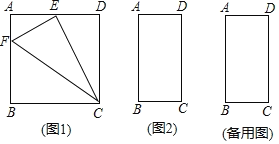
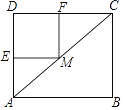
【题目】如图，在矩形ABCD中，AB=8，AD=6，点M为对角线AC上的一个动点（不与端点A，C重合），过点M作ME⊥AD，MF⊥DC，垂足分别为E，F，则四边形EMFD面积的最大值为（ ）

A. 6 B. 12 C. 18 D. 24

【答案】B

【解析】

根据矩形的性质和判定可得四边形EBFM是矩形，根据相似三角形的判定和性质可得设DF=EM=x，DE=FM=y，得到 根据矩形的面积公式得到四边形EMFD面积

再根据函数的最值问题即可求解．

∵四边形ABCD是矩形，

∴

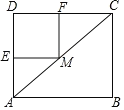
∵ME⊥AD，MF⊥DC，

∴

∴四边形EBFM是矩形；

∴DF=EM,DE=FM,FM∥AD,ME∥CD，

∴△AEM∽△ADC，

∴

设DF=EM=x，DE=FM=y，

∴

四边形EMFD面积

故x=4时，四边形EMFD面积的最大值为12.

故选：B.

练习册系列答案
相关题目

【题目】已知如图，矩形OABC的长OA=，宽OC=1，将△AOC沿AC翻折得△APC．

（1）求∠PCB的度数；

（2）若P，A两点在抛物线y=﹣x2+bx+c上，求b，c的值，并说明点C在此抛物线上；

（3）（2）中的抛物线与矩形OABC边CB相交于点D，与x轴相交于另外一点E，若点M是x轴上的点，N是y轴上的点，以点E、M、D、N为顶点的四边形是平行四边形，试求点M、N的坐标．

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．

（1）当t为何值时，AD=AB，并求出此时DE的长度；

（2）当△DEG与△ACB相似时，求t的值．

【题目】方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示．解答问题：

（1）请按要求对△ABO作如下变换：

①将△OAB向下平移2个单位，再向左平移3个单位得到△O1A1B1；

②以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA2B2．

（2）写出点A1，A2的坐标： ， ；

（3）△OA2B2的面积为 ．

【题目】如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x2+bx+c经过B点，且与x轴交于C，D两点（点C在左侧），且C(-3，0)．

（1）求抛物线的解析式；

（2）平移直线AB，使得平移后的直线与抛物线分别交于点D，E，与y轴交于点F，连接CE，CF，求△CEF的面积．

【题目】已知：如图，在△ABC中，AB=AC，DE∥BC，点F在边AC上，DF与BE相交于点G，且∠EDF=∠ABE．

求证：（1）△DEF∽△BDE；（2）DGDF=DBEF．

【题目】在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax2﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（　　）

A. a≤﹣1或≤a＜ B. ≤a＜

C. a≤或a＞ D. a≤﹣1或a≥

【题目】一个四边形被一条对角线分割成两个三角形，如果被分割的两个三角形相似，我们把这条对角线称为该四边形的为相似对角线。

(1)如图1，正方形ABCD的边长为4，E为AD的中点，AF=1，连结CE，CF，求证：EF为四边形AECF的相似对角线。

(2)在四边形ABCD中,∠BAD=120°,AB=3,AC=，AC平分∠BAD，且AC是四边形ABCD的相似对角线，求BD的长。

(3)如图2,在矩形ABCD中,AB=6,BC=4,点E是线段AB(不取端点A,B)上的一个动点,点F是射线AD上的一个动点,若EF是四边形AECF的相似对角线,求BE的长.(直接写出答案)

【题目】如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2).

(1)将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形.

(2)平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A2B2C2的图形.

(3)若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网