题目内容
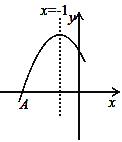
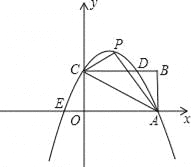
【题目】已知如图,矩形OABC的长OA=![]() ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=﹣![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
【答案】
【1】 ∠PCB=30°
【2】 ![]() 点C(0,1)满足上述函数关系式,所以点C在抛物线上.
点C(0,1)满足上述函数关系式,所以点C在抛物线上.
【3】 Ⅰ、若DE是平行四边形的对角线,点C在y轴上,CD平行x轴,
∴过点D作DM∥ CE交x轴于M,则四边形EMDC为平行四边形,
把y=1代入抛物线解析式得点D的坐标为(![]() ,1)
,1)
把y=0代入抛物线解析式得点E的坐标为(![]() ,0)
,0)
∴M(![]() ,0);N点即为C点,坐标是(0,1); ……9分
,0);N点即为C点,坐标是(0,1); ……9分
Ⅱ、若DE是平行四边形的边,
则DE=2,∠DEF=30°,
过点A作AN∥DE交y轴于N,四边形DANE是平行四边形,
∴M(![]() ,0),N(0,-1); ……11分
,0),N(0,-1); ……11分
同理过点C作CM∥DE交y轴于N,四边形CMDE是平行四边形,
∴M(![]() ,0),N(0, 1). ……12分
,0),N(0, 1). ……12分
【解析】
(1)根据OC、OA的长,可求得∠OCA=∠ACP=60°(折叠的性质),∠BCA=∠OAC=30°,由此可判断出∠PCB的度数.
(2)过P作PQ⊥OA于Q,在Rt△PAQ中,易知PA=OA=3,而∠PAO=2∠PAC=60°,即可求出AQ、PQ的长,进而可得到点P的坐标,将P、A坐标代入抛物线的解析式中,即可得到b、c的值,从而确定抛物线的解析式,然后将C点坐标代入抛物线的解析式中进行验证即可.
(3)根据抛物线的解析式易求得C、D、E点的坐标,然后分两种情况考虑:
①DE是平行四边形的对角线,由于CD∥x轴,且C在y轴上,若过D作直线CE的平行线,那么此直线与x轴的交点即为M点,而N点即为C点,D、E的坐标已经求得,结合平行四边形的性质即可得到点M的坐标,而C点坐标已知,即可得到N点的坐标;
②DE是平行四边形的边,由于A在x轴上,过A作DE的平行线,与y轴的交点即为N点,而M点即为A点;易求得∠DEA的度数,即可得到∠NAO的度数,已知OA的长,通过解直角三角形可求得ON的值,从而确定N点的坐标,而M点与A点重合,其坐标已知;
同理,由于C在y轴上,且CD∥x轴,过C作DE的平行线,也可找到符合条件的M、N点,解法同上.
解:(1)在Rt△OAC中,OA=![]() ,OC=1,则∠OAC=30°,∠OCA=60°;
,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP=![]() ,∠ACO=∠ACP=60°;
,∠ACO=∠ACP=60°;
∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°.
(2)过P作PQ⊥OA于Q;
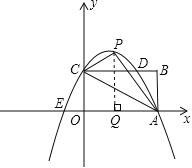
Rt△PAQ中,∠PAQ=60°,AP=![]() ;
;
∴OQ=AQ=![]() ,PQ=
,PQ=![]() ,
,
所以P(![]() ,
,![]() );
);
将P、A代入抛物线的解析式中,得:
 ,
,
解得![]() ;
;
即y=-![]() x2+
x2+![]() x+1;
x+1;
当x=0时,y=1,故C(0,1)在抛物线的图象上.
(3)①若DE是平行四边形的对角线,点C在y轴上,CD平行x轴,
∴过点D作DM∥CE交x轴于M,则四边形EMDC为平行四边形,
把y=1代入抛物线解析式得点D的坐标为(![]() ,1)
,1)
把y=0代入抛物线解析式得点E的坐标为(-![]() ,0)
,0)
∴M(![]() ,0);N点即为C点,坐标是(0,1);
,0);N点即为C点,坐标是(0,1);

②若DE是平行四边形的边,
过点A作AN∥DE交y轴于N,四边形DANE是平行四边形,
∴DE=AN=![]() =
=![]() =2,
=2,
∵tan∠EAN=![]() =
=![]() ,
,
∴∠EAN=30°,
∵∠DEA=∠EAN,
∴∠DEA=30°,
∴M(,0),N(0,-1);
同理过点C作CM∥DE交y轴于N,四边形CMDE是平行四边形,
∴M(-![]() ,0),N(0,1).
,0),N(0,1).

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案