ΧβΡΩΡΎ»ί
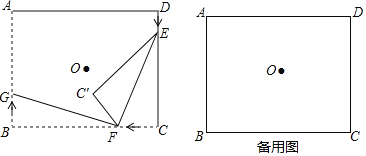
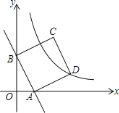
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§AC=3Θ§BC=4Θ§ΙΐΒψBΉς…δœΏBB1ΓΈACΘ°Ε·ΒψD¥”ΒψA≥ωΖΔ―Ί…δœΏACΖΫœρ“‘ΟΩΟκ5ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±Ε·ΒψE¥”ΒψC―Ί…δœΏACΖΫœρ“‘ΟΩΟκ3ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·Θ°ΙΐΒψDΉςDHΓΆAB”ΎHΘ§ΙΐΒψEΉςEFΓΆACΫΜ…δœΏBB1”ΎFΘ§G «EF÷–ΒψΘ§Ν§Ϋ”DGΘ°…ηΒψD‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ°
Θ®1Θ©Β±tΈΣΚΈ÷Β ±Θ§AD=ABΘ§≤Δ«σ≥ω¥Υ ±DEΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©Β±ΓςDEG”κΓςACBœύΥΤ ±Θ§«σtΒΡ÷ΒΘ°
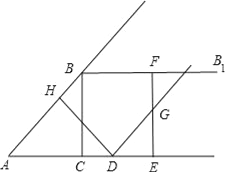
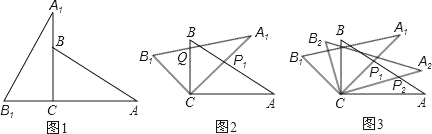
ΓΨ¥πΑΗΓΩΘ®1Θ©Β±t=1 ±Θ§AD=ABΘ§AE=1ΘΜ
Θ®2Θ©Β±t=![]() Μρ
Μρ ![]() Μρ
Μρ ![]() Μρ
Μρ ![]() ±Θ§ΓςDEG”κΓςACBœύΥΤ.
±Θ§ΓςDEG”κΓςACBœύΥΤ.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΙ¥Ι…Ε®άμΒΟ≥ωAB=5,“Σ ΙAD=AB=5Θ§ΓΏΕ·ΒψDΟΩΟκ5ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·Θ§Γύt=1ΘΜΘ®2Θ©Β±ΓςDEG”κΓςACBœύΥΤ ±Θ§“ΣΖ÷ΝΫ÷÷«ιΩωΧ÷¬έΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ν–≥ω±»άΐ ΫΘ§«σ≥ωDEΒΡ±μ¥ο Ϋ ±Θ§“ΣΖ÷ADΘΦAEΚΆADΘΨAEΝΫ÷÷«ιΩωΧ÷¬έ.
‘ΧβΫβΈωΘΚ
Θ®1Θ©ΓΏΓœACB=90ΓψΘ§AC=3Θ§BC=4Θ§ ΓύAB=![]() =5Θ°
=5Θ°
ΓΏAD=5tΘ§CE=3tΘ§ ΓύΒ±AD=AB ±Θ§5t=5Θ§Φ¥t=1ΘΜ
ΓύAE=AC+CE=3+3t=6Θ§DE=6©¹5=1Θ°
Θ®2Θ©ΓΏEF=BC=4Θ§G «EFΒΡ÷–ΒψΘ§ ΓύGE=2Θ°
Β±ADΘΦAEΘ®Φ¥tΘΦ![]() Θ© ±Θ§DE=AE©¹AD=3+3t©¹5t=3©¹2tΘ§
Θ© ±Θ§DE=AE©¹AD=3+3t©¹5t=3©¹2tΘ§
»τΓςDEG”κΓςACBœύΥΤΘ§‘ρ ![]() Μρ
Μρ ![]() Θ§
Θ§
Γύ![]() Μρ
Μρ![]() Θ§ Γύt=
Θ§ Γύt=![]() Μρt=
Μρt=![]() ΘΜ
ΘΜ
Β±ADΘΨAEΘ®Φ¥tΘΨ![]() Θ© ±Θ§DE=AD©¹AE=5t©¹Θ®3+3tΘ©=2t©¹3Θ§
Θ© ±Θ§DE=AD©¹AE=5t©¹Θ®3+3tΘ©=2t©¹3Θ§
»τΓςDEG”κΓςACBœύΥΤΘ§‘ρ ![]() Μρ
Μρ ![]() Θ§ Γύ
Θ§ Γύ![]() Μρ
Μρ![]() Θ§
Θ§
ΫβΒΟt=![]() Μρt=
Μρt=![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘ§Β±t=![]() Μρ
Μρ ![]() Μρ
Μρ ![]() Μρ
Μρ ![]() ±Θ§ΓςDEG”κΓςACBœύΥΤΘ°
±Θ§ΓςDEG”κΓςACBœύΥΤΘ°

 ÷–ΩΦΫβΕΝΩΦΒψΨΪΝΖœΒΝ–¥πΑΗ
÷–ΩΦΫβΕΝΩΦΒψΨΪΝΖœΒΝ–¥πΑΗ ΗςΒΊΤΎΡ©Η¥œΑΧΊ―ΒΨμœΒΝ–¥πΑΗ
ΗςΒΊΤΎΡ©Η¥œΑΧΊ―ΒΨμœΒΝ–¥πΑΗ –Γ≤© ΩΤΎΡ©¥≥ΙΊ100Ζ÷œΒΝ–¥πΑΗ
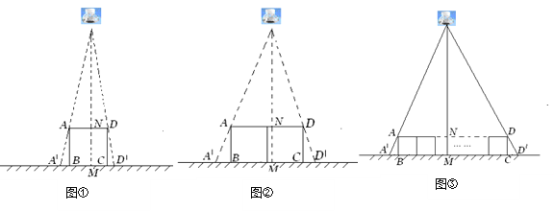
–Γ≤© ΩΤΎΡ©¥≥ΙΊ100Ζ÷œΒΝ–¥πΑΗΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥«χΑΥΡξΦΕ―ß…ζΒΡΥ·ΟΏ«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥΗΟ«χΑΥΡξΦΕ―ß…ζ≤ΩΖ÷―ß…ζΫχ––Βς≤ι.“―÷ΣDΉιΒΡ―ß…ζ”–15»ΥΘ§άϊ”Ο≥ι―υΥυΒΟΒΡ ΐΨίΜφ÷ΤΥυ ΨΒΡΆ≥ΦΤΆΦ±μ.
“ΜΓΔ―ß…ζΥ·ΟΏ«ιΩωΖ÷Ήι±μΘ®ΒΞΈΜΘΚ–Γ ±Θ©
Ήι±π | Υ·ΟΏ ±Φδ |
|
|
|
|
|
|
|
|
|
|
ΕΰΓΔ―ß…ζΥ·ΟΏ«ιΩωΆ≥ΦΤΆΦ
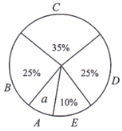
ΗυΨίΆΦ±μΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ© ‘«σΓΑΑΥΡξΦΕ―ß…ζΥ·ΟΏ«ιΩωΆ≥ΦΤΆΦΓ±÷–ΒΡaΒΡ÷ΒΦΑaΕ‘”ΠΒΡ…»–ΈΒΡ‘≤–ΡΫ«Ε» ΐΘΜ
Θ®2Θ©»γΙϊΥ·ΟΏ ±ΦδxΘ® ±Θ©¬ζΉψΘΚ![]() Θ§≥ΤΥ·ΟΏ ±ΦδΚœΗώ.“―÷ΣΗΟ«χΑΥΡξΦΕ―ß…ζ”–3250»ΥΘ§ ‘ΙάΦΤΗΟ«χΑΥΡξΦΕ―ß…ζΥ·ΟΏ ±ΦδΚœΗώΒΡΙ≤”–Εύ…Ό»ΥΘΩ
Θ§≥ΤΥ·ΟΏ ±ΦδΚœΗώ.“―÷ΣΗΟ«χΑΥΡξΦΕ―ß…ζ”–3250»ΥΘ§ ‘ΙάΦΤΗΟ«χΑΥΡξΦΕ―ß…ζΥ·ΟΏ ±ΦδΚœΗώΒΡΙ≤”–Εύ…Ό»ΥΘΩ
Θ®3Θ©»γΙϊΫΪΗςΉι±π―ß…ζΥ·ΟΏ«ιΩωΖ÷ΉιΒΡΉν–Γ÷ΒΘ®»γCΉι±π÷–Θ§»Γ![]() Θ©Θ§BΓΔCΓΔD»ΐΉι―ß…ζΒΡΤΫΨυΥ·ΟΏ ±ΦδΉςΈΣΑΥΡξΦΕ―ß…ζΒΡΥ·ΟΏ ±ΦδΒΡ“άΨί. ‘«σΗΟ«χΑΥΡξΦΕ―ß…ζΒΡΤΫΨυΥ·ΟΏ ±Φδ.
Θ©Θ§BΓΔCΓΔD»ΐΉι―ß…ζΒΡΤΫΨυΥ·ΟΏ ±ΦδΉςΈΣΑΥΡξΦΕ―ß…ζΒΡΥ·ΟΏ ±ΦδΒΡ“άΨί. ‘«σΗΟ«χΑΥΡξΦΕ―ß…ζΒΡΤΫΨυΥ·ΟΏ ±Φδ.