题目内容
【题目】一个四边形被一条对角线分割成两个三角形,如果被分割的两个三角形相似,我们把这条对角线称为该四边形的为相似对角线。
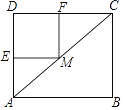
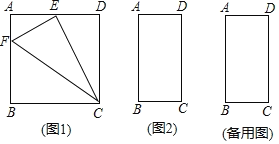
(1)如图1,正方形ABCD的边长为4,E为AD的中点,AF=1,连结CE,CF,求证:EF为四边形AECF的相似对角线。
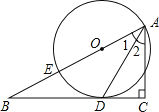
(2)在四边形ABCD中,∠BAD=120°,AB=3,AC=![]() ,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
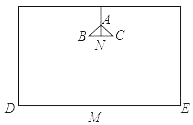
(3)如图2,在矩形ABCD中,AB=6,BC=4,点E是线段AB(不取端点A,B)上的一个动点,点F是射线AD上的一个动点,若EF是四边形AECF的相似对角线,求BE的长.(直接写出答案)
【答案】(1)见解析 (2)3![]() 或
或![]() . (3)
. (3)![]() 或3
或3
【解析】
(1)如图1中,只要证明△AEF∽△ECF即可解决问题;
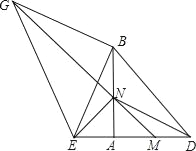
(2)如图2、图3中,AC是四边形ABCD的相似对角线,有两种情形:①如图2中,△ACB≌△ACD时.②如图3中,当△ACD∽△ABC时,分别求解即可;
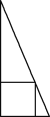
(3)分三种情形①如图4中,当△AEF和△CEF关于EF对称时,EF是四边形AECF的相似对角线.②如图5中,如图取AD中点F,连接CF,将△CFD沿CF翻折得到△CFD′,延长CD′交AB于E,易证EF是四边形AECF的相似对角线.③如图6中,取AB的中点E,连接CE,作EF⊥AD于F,延长CB交FE的延长线于M,则易证EF是四边形AECF的相似对角线.此时BE=3;
(1)如图1中,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,
∵AE=DE=2,AF=1,
∴![]() ,
,
∵∠A=∠D=90°,
∴△AEF∽△DCE,
∴∠AEF=∠DCE,![]() ,
,
∵∠DCE+∠CED=90°,
∴∠AEF+∠CED=90°,
∴∠FEC=∠A=90°,
∵![]() ,
,
∴![]() ,
,
∴△AEF∽△ECF,
∴EF为四边形AECF的相似对角线.
(2)如图2中,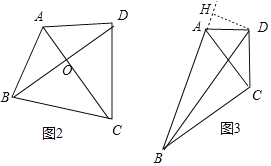
∵AC是四边形ABCD的相似对角线,
∴有两种情形:
①如图2中,△ACB≌△ACD时,∵AB=AD=3,BC=CD,
∴AC垂直平分DB,
在Rt△AOB中,∵AB=3,∠ABO=30°,
∴BO=ABcos30°=![]() ,
,
∴BD=2OB=3![]() .
.
②如图3中,当△ACD∽△ABC时,可得AC2=ABAD,
∴6=3AD,
∴AD=2,
在Rt△ADH中,∵∠HAD=60°,AD=2,
∴AH=![]() AD=1,DH=
AD=1,DH=![]() AH=
AH=![]() ,
,
在Rt△BDH中,BD=![]() .
.
综上所述,BD=3![]() 或
或![]() .
.
(3)①如图4中,当△AEF和△CEF关于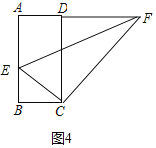
设AE=EC=x,
在Rt△BCE中,∵EC2=BE2+BC2,
∴x2=(6-x)2+42,解得x=![]() ,
,
∴此时BE=AB-AE=6-![]() .
.
②如图5中,如图取AD中点F,连接CF,将△CFD沿CF翻折得到△CFD′,延长CD′交AB于E,易证EF是四边形AECF的相似对角线.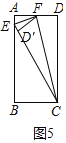
由△AEF∽△DFC得到,![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴BE=AB-AE=![]() .
.
③如图6中,取AB的中点E,连接CE,作EF⊥EC交AD于F,延长CB交FE的延长线于M,则易证EF是四边形AECF的相似对角线.此时BE=3.
综上所述,满足条件的BE的值为![]() 或3.
或3.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案