题目内容
如图，△ABC的中线AF与中位线DE相交于点O，连接DF、EF．
（1）试判断四边形ADFE的形状？并说明理由．
（2）试探究：△ABC满足什么条件时，四边形ADFE是菱形？并请说明理由．
（1）试判断四边形ADFE的形状？并说明理由．
（2）试探究：△ABC满足什么条件时，四边形ADFE是菱形？并请说明理由．
（1）四边形ADFE是平行四边形；
理由：∵△ABC的中线AF与中位线DE相交于点O，
∴EF是△ABC的中位线，AD=BD，
∴EF∥AB，EF=
AB，
∴AD
EF，
∴四边形ADFE是平行四边形；
（2）当△ABC是等腰三角形时，四边形ADFE是菱形，
理由：∵△ABC是等腰三角形，
∴AB=AC，DE是△ABC的中位线，
∴AD=AE，
∴平行四边形ABCD是菱形．
理由：∵△ABC的中线AF与中位线DE相交于点O，
∴EF是△ABC的中位线，AD=BD，
∴EF∥AB，EF=
| 1 |
| 2 |
∴AD
| ∥ |
| . |
∴四边形ADFE是平行四边形；
（2）当△ABC是等腰三角形时，四边形ADFE是菱形，
理由：∵△ABC是等腰三角形，
∴AB=AC，DE是△ABC的中位线，
∴AD=AE，
∴平行四边形ABCD是菱形．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
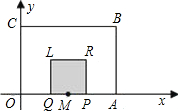Q为一边向上作正方形PRLQ．设点P的运动时间为t（秒），正方形PRLQ与矩形OABC重叠部分（阴影部分）的面积为S（平方单位）．
