题目内容
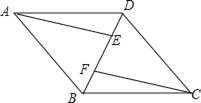
【题目】已知△ABC为边长为6的等边三角形,D,E分别在边BC,AC上,且CD=CE=x,连接DE并延长至点F,使EF=AE,连接AF,CF.
(1)求证:△AEF为等边三角形;
(2)求证:四边形ABDF是平行四边形;
(3)记△CEF的面积为S,
①求S与x的函数关系式;
②当S有最大值时,判断CF与BC的位置关系,并说明理由.
【答案】
(1)证明:∵△ABC为等边三角形,
∴AB=AC=BC,∠ACB=60°,
∵CD=CE,
∴△CDE为等边三角形,
∴∠CED=60°,
∠AEF=60°,又AE=EF,
∴△AEF为等边三角形
(2)证明:∵∠FAC=60°,
∴∠FAC=∠ACB=60°,
∴AF∥BC,
∵∠CED=∠CAB=60°,
∴AB∥BF,()
∴四边形ABDF为平行四边形
(3)证明:①作AH⊥BC于H,
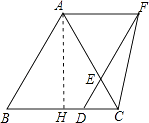
∵△ABC为边长为6的等边三角形,
∴AH=3 ![]() ,
,
∴S△CDF= ![]() ×CD×AH=
×CD×AH= ![]() x,
x,
∵△CDE为等边三角形,CD=x,
∴S△CDE= ![]() x2,
x2,
∴△CEF的面积S= ![]() x﹣
x﹣ ![]() x2;
x2;
②CF⊥BC.
x=﹣ ![]() =3时,S最大,
=3时,S最大,
∴CD=CE=3,
∵△CDE为等边三角形,
∴DE=CD=CE=3,
∵E为AC的中点,
∴AE=CE=3
∴AE=EF=3
∴CE=DE=EF=3,
∴∠CDE=∠ECD,
∠ECF=∠EFC,
∵∠CDE+∠ECD+∠CCF+∠EFC=180°,
∴2∠ECD+2∠ECF=180°,
∴∠ECD+∠ECF=90°,即∠DCF=90°,
∴CF⊥BC.
【解析】(1)根据等边三角形的性质得出∠ACB=60°,由CD=CE及EF=AE,根据对顶角相等和等边三角形的判定定理证明即可;
(2)根据两组对边分别平行的四边形是平行四边形,已征得结论;
(3)观察图形S=S△CDF-S△CDE,根据等边三角形的性质可以分别求出△CDF,△CDE的面积,就可以计算出求S与x的函数关系式;根据二次函数的性质求出S的最大值时x的值,根据垂直的定义判断即可。
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a),还要掌握平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形)的相关知识才是答题的关键.

【题目】成都市的水费实行下表的收费方式:
每月用水量 | 单价 |
不超出 | 2元/ |
超出 | 3元/ |
超出 | 4元/ |
(1)周老师家九月份用了![]() 的水,应付多少水费?
的水,应付多少水费?
(2)如果李老师家九月份的用水量为![]() ,那么应付的水费为多少元?
,那么应付的水费为多少元?
(3)如果曹老师家九月和十月一共用了![]() 的水,且已知九月比十月少,设九月用水量为
的水,且已知九月比十月少,设九月用水量为![]() ,那么曹老师这两个月一共要交多少钱的水费?(可用含
,那么曹老师这两个月一共要交多少钱的水费?(可用含![]() 的代数式表示)
的代数式表示)