题目内容
【题目】如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是 . 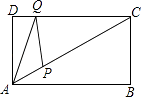
【答案】4 ![]()
【解析】解:以CD为轴,将△ACD往上翻转180°,如图,
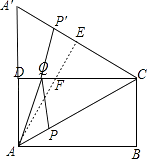
过点A作AE⊥A′C于E点,AE交CD于F点,
当Q与F点重合,P′与E点重合时,AQ+QP=AF+EF=AE最短(直线外一点到这条直线中,垂线段最短),
∵矩形ABCD中,AD=4,∠CAB=30°,
∴∠A′CD=∠ACD=∠CAB=30°,3
∴∠A′CA=60°,
又∵AC=A′C,
∴△A′CA为等边三角形,且A′A=2AD=8,
AE=A′Asin∠A′CA=8× ![]() =4
=4 ![]() .
.
故答案为:4 ![]() .
.
这是一道双动点问题,以CD为轴,将ACD往上翻转180°,由已知矩形ABCD中,∠CAB=30°,可以得到∠A′AC=60°,易证得△A′AC是等边三角形,求出边A′C上的高,由两点之间线段最短即可得出结论。也可以作点A关于点D的中心对称点A′,过点A′作AC的垂线即可。

【题目】某数码专营店销售甲、乙两种品牌智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4300 | 3600 |
售价(元/部) | 4800 | 4200 |
(1)该店销售记录显示.三月份销售甲、乙两种手机共17部,且销售甲种手机的利润恰好是销售乙种手机利润的2倍,求该店三月份售出甲种手机和乙种手机各多少部?
(2)根据市场调研,该店四月份计划购进这两种手机共20部,要求购进乙种手机数不超过甲种手机数的![]() ,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
(3)在(2)的条件下,该店打算将四月份按计划购进的20部手机全部售出后,所获得利润的30%用于购买A,B两款教学仪器捐赠给某希望小学.已知购买A仪器每台300元,购买B仪器每台570元,且所捐的钱恰好用完,试问该店捐赠A,B两款仪器一共多少台?(直接写出所有可能的结果即可)