��Ŀ����
����Ŀ����ͼ1����֪����ֱ��AB��CD��ֱ��EF���أ��ֱ��ڵ�E����F��EMƽ�֡�AEF��CD�ڵ�M���ҡ�FEM����FME��

��1��ֱ��AB��ֱ��CD�Ƿ�ƽ�У�˵��������ɣ�
��2����ͼ2����G������MD��һ���㣨�����M��F�غϣ���EHƽ�֡�FEG��CD�ڵ�H������H��HN��EM�ڵ�N�����EHN��������EGF���£�
�ٵ���G�ڵ�F���Ҳ�ʱ�����£�60�㣬����Ķ�����
�ڵ���G���˶������У����ͦ�֮����������������ϵ����д����IJ��룬������֤����
���𰸡���1��AB��CD�����ɼ���������2����30�㣻�ڦ���![]() �£�֤��������.
�£�֤��������.
��������
��1�����ݽ�ƽ���ߵ����ʼ���������֤����AEM����FME���ɣ�
��2���ٸ���ƽ���ߵ��������BEG������ƽ�ǵĶ��������AEG�Ķ��������ݽ�ƽ���ߵĶ��������HEN���ɽ�����⣮
�ڽ��ۣ���=![]() ��������ƽ���ߵ��������BEG������ƽ�ǵĶ����ʾ��AEG�Ķ��������ݽ�ƽ���ߵĶ����ʾ��HEN���ɽ�����⣮
��������ƽ���ߵ��������BEG������ƽ�ǵĶ����ʾ��AEG�Ķ��������ݽ�ƽ���ߵĶ����ʾ��HEN���ɽ�����⣮
��1�����ۣ�AB��CD��
���ɣ���ͼ1�У�
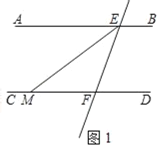
��EMƽ�֡�AEF��CD�ڵ�M��
���AEM����MEF��
�ߡ�FEM����FME��
���AEM����FME��
��AB��CD��
��2������ͼ2�У�
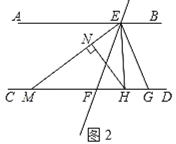
��AB��CD��
���BEG����EGF������60��
���AEG��120����
��EHƽ�֡�FEG��EMƽ�֡�AEF
���HEF����HEG����AEM����MEF
���HEN����MEF+��HEF��![]() ��AEG��60����
��AEG��60����
��HN��EM��
���HNE��90����
���EHN��90������HEN��30����
�ڲ��룺����![]() ����
����
���ɣ���AB��CD��
���BEG����EGF������
���AEG��180��������
��EHƽ�֡�FEG��EMƽ�֡�AEF
���HEF����HEG����AEM����MEF
���HEN����MEF+��HEF��![]() ��AEG��90����
��AEG��90����![]() ��
��
��HN��EM��
���HNE��90����
��������EHN��90������HEN��![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij�̳���̨����ÿ̨���۷ֱ�Ϊ160Ԫ��120Ԫ��![]() ��
��![]() �����ͺŵĵ������±��ǽ����ܵ����������
�����ͺŵĵ������±��ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
|
| ||
��һ�� | 3̨ | 4̨ | 1200Ԫ |
�ڶ��� | 5̨ | 6̨ | 1900Ԫ |
�����ۡ��ۼ۾����ֲ��䣬�����������롪�����ɱ���
��1����![]() ��
��![]() �����ͺŵĵ��������۵��ۣ�
�����ͺŵĵ��������۵��ۣ�
��2�����̳����ò�����7500Ԫ�Ľ���ٲɹ��������ͺŵĵ�����50̨����![]() ���ͺŵĵ�������ܲɹ�����̨��
���ͺŵĵ�������ܲɹ�����̨��
��3���ڣ�2�����̳��ò�����7500Ԫ�ɹ��������ͺŵĵ�����50̨�������£��̳���������50̨�����ܷ�ʵ������1850Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵������.
����Ŀ��ij����רӪ�����ۼס�������Ʒ�������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4300 | 3600 |
�ۼۣ�Ԫ/���� | 4800 | 4200 |
��1���õ����ۼ�¼��ʾ�����·����ۼס��������ֻ���17���������ۼ����ֻ�������ǡ�������������ֻ������2������õ����·��۳������ֻ��������ֻ������ٲ���
��2�������г����У��õ����·ݼƻ������������ֻ���20����Ҫ�������ֻ��������������ֻ�����![]() �������ڹ����������ֻ����ʽ����81500Ԫ����ͨ������������п��ܵĽ���������
�������ڹ����������ֻ����ʽ����81500Ԫ����ͨ������������п��ܵĽ���������
��3���ڣ�2���������£��õ���㽫���·ݰ��ƻ�������20���ֻ�ȫ���۳�������������30%���ڹ���A��B�����ѧ����������ijϣ��Сѧ����֪����A����ÿ̨300Ԫ������B����ÿ̨570Ԫ���������Ǯǡ�����꣬���ʸõ����A��B��������һ������̨����ֱ��д�����п��ܵĽ�����ɣ�



