Question

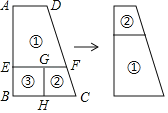
【题目】如图，梯形ABCD被分割成两个小梯形①②，和一个小正方形③，去掉③后，①和②可剪拼成一个新的梯形，若EF﹣AD＝2，BC﹣EF＝1，则AB的长是（ ）

A.6B.3C.9D.3

Answer 1

【答案】C

【解析】

连接AH交EF于点K，根据EF﹣AD＝2，BC﹣EF＝1，可得BC﹣AD＝3，由图象剪拼观察可得，AD＝HC，四边形AHCD是平行四边形，再证明△AEK∽△ABH，可得AB的长．

解：如图，

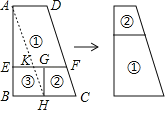
连接AH交EF于点K，

∵EF﹣AD＝2，BC﹣EF＝1，

∴BC﹣AD＝3，

由图象剪拼观察可知：

AD＝HC，

∴四边形AHCD是平行四边形，

∴BC﹣AD＝BC﹣HC＝3，

KF＝AD，EK＝2，

∵③为正方形，

∴EB＝BH＝3，

∵EK∥BH，

∵△AEK∽△ABH，

∴，

即，

解得AB＝9．

故选：C．