题目内容
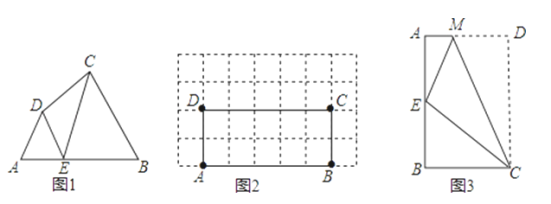
【题目】如图,在△ABC中,BC=5,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=![]() CE时,EP+BP的值为( )
CE时,EP+BP的值为( )
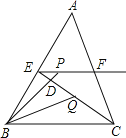
A.10B.8C.6D.5
【答案】A
【解析】
延长BQ交射线EF于M,根据三角形的中位线平行于第三边可得EF∥BC,根据两直线平行,内错角相等可得∠M=∠CBM,再根据角平分线的定义可得∠PBM=∠CBM,从而得到∠M=∠PBM,根据等角对等边可得BP=PM,求出EP+BP=EM,再根据CQ=![]() CE求出EQ=2CQ,然后根据△MEQ和△BCQ相似,利用相似三角形对应边成比例列式求解即可.
CE求出EQ=2CQ,然后根据△MEQ和△BCQ相似,利用相似三角形对应边成比例列式求解即可.
解:如图,延长BQ交射线EF于M,
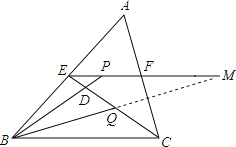
∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠M=∠CBM,
∵BQ是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴EP+BP=EP+PM=EM,
∵CQ=![]() CE,
CE,
∴EQ=2CQ,
由EF∥BC得,△MEQ∽△BCQ,
![]() ,
,
∴EM=2BC=2×5=10,
即EP+BP=10.
故选:A.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目