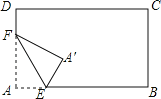
题目内容
【题目】如图,在平行四边形ABCD中,∠B<90,BC>AB.作AE⊥BC于点E,AF⊥CD于点F,记∠EAF的度数为α,AE=a,AF=b.则以下选项错误的是( )

A. ∠D的度数为α
B. a∶b=CD∶BC
C. 若α=60,则平行四边形ABCD的周长为 ![]()
D. 若α=60,则四边形AECF的面积为平行四边形ABCD面积的一半
【答案】D
【解析】
A.根据垂直定义和四边形内角和得∠α+∠C=180°,再由平行四边形性质得∠C+∠D=180°,等量代换即可得∠D=∠α,故正确;
B. 由平行四边形面积公式可得BC·a=CD·b,即CD:BC=a:b,故正确;
C.由A知∠B=∠D=60°,在Rt△ABE、Rt△ADF中,根据勾股定理可得AB=![]() a,AD=
a,AD=![]() b, 根据平行四边形周长公式即可求得C四边形ABCD=
b, 根据平行四边形周长公式即可求得C四边形ABCD=![]() (a+b),故正确;
(a+b),故正确;
D.由C知AB=![]() a,AD=
a,AD=![]() b,从而可得BE=
b,从而可得BE=![]() a,DF=
a,DF=![]() b,根据三角形面积 公式分别求得S△ABE=
b,根据三角形面积 公式分别求得S△ABE=![]() a2,S△ADF=
a2,S△ADF=![]() b2,由S四边形AECF=S四边形ABCD-S△ABE-S△ADF=
b2,由S四边形AECF=S四边形ABCD-S△ABE-S△ADF=![]() ab-
ab-![]() a2-
a2-![]() b2,故错误.
b2,故错误.
解:A.∵ AE⊥BC , AF⊥CD ,
∴∠AEC=∠AFC=90°,
∴∠α+∠C=180°,
∵四边形ABCD是平行四边形,
∴∠C+∠D=180°,
∴∠D=∠α,故正确,A不符合题意;
B.∵ AE⊥BC , AF⊥CD ,
∴S四边形ABCD=BC·AE=CD·AF,
∵ AE=a,AF=b,
∴BC·a=CD·b,
即CD:BC=a:b,故正确,B不符合题意;
C.由A知∠D=∠α,
∵四边形ABCD是平行四边形,∠α=60°,
∴∠B=∠D=60°,
∵AE⊥BC ,
∴∠AEC=90°,
∴∠BAE=30°,
在Rt△ABE中,
∵AE=a ,
∴BE=![]() AB,AB2=BE2+AE2 ,
AB,AB2=BE2+AE2 ,
即AB2=(![]() AB)2+a2 ,
AB)2+a2 ,
解得:AB=![]() a,
a,
∵ AF⊥CD ,∴∠AFC=90°,
∴∠DAF=30°,
在Rt△ADF中,
∵AF=b ,
∴DF=![]() AD,AD2=DF2+AF2 ,
AD,AD2=DF2+AF2 ,
即AD2=(![]() AD)2+b2 ,
AD)2+b2 ,
解得:AD=![]() b,
b,
∴C四边形ABCD=2(AB+AD)=2×(![]() a+
a+![]() b)=
b)=![]() (a+b),
(a+b),
故正确,C不符合题意;
D.由C知AB=![]() a,AD=
a,AD=![]() b,
b,
∴BE=![]() a,DF=
a,DF=![]() b,
b,
∴S△ABE=![]() ·BE·AE=
·BE·AE=![]() ×
×![]() a×a=
a×a=![]() a2 ,
a2 ,
S△ADF=![]() ·DF·AF=
·DF·AF=![]() ×
×![]() b×b=
b×b=![]() b2 ,
b2 ,
∵S四边形ABCD=BC·AE=![]() ab,
ab,
∴S四边形AECF=S四边形ABCD-S△ABE-S△ADF ,
=ab-
![]() a2-
a2-![]() b2 ,
b2 ,
故错误,D符合题意;
故答案为:D.

【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
【题目】用火柴棒按下列方式搭建三角形:

(1)填表:
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)当三角形的个数为![]() 时,火柴棒的根数是多少?
时,火柴棒的根数是多少?
(3)求当![]() 时,有多少根火柴棒?
时,有多少根火柴棒?
(4)当火柴棒的根数为2017时,三角形的个数是多少?
【题目】从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在实验中得到下列表中部分数据:
实验次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
出现方块的次数 | 11 | 18 | a | 40 | 49 | 63 | 68 | 80 | 91 | 100 |
出现方块的频率 | 27.5% | 22.5% | 25% | 25% | 24.5% | 26.25% | 24.3% | b | 25% | 25% |
(1)填空a= ,b= ;
(2)从上面的图表中可以估计出现方块的概率是 ;
(3)将这幅扑克中的所有方块(即从方块1到方块13,共13张)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗说明理由.