题目内容
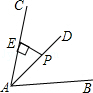
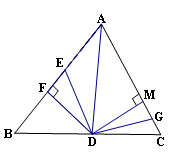
如图,在 中,
中,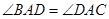 ,
,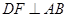 ,
,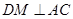 ,AF=10cm, AC=14cm,动点E以2cm/s的速度从
,AF=10cm, AC=14cm,动点E以2cm/s的速度从 点向
点向 点运动,动点
点运动,动点 以1cm/s的速度从
以1cm/s的速度从 点向
点向 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
(1)求证:在运动过程中,不管t取何值,都有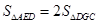 ;
;
(2)当t取何值时,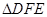 与
与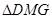 全等;
全等;
(3)在(2)的前提下,若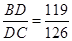 ,
,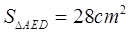 ,求
,求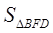 。
。
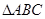 中,
中,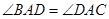 ,
,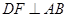 ,
,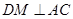 ,AF=10cm, AC=14cm,动点E以2cm/s的速度从
,AF=10cm, AC=14cm,动点E以2cm/s的速度从 点向
点向 点运动,动点
点运动,动点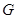 以1cm/s的速度从
以1cm/s的速度从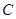 点向
点向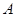 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
(1)求证:在运动过程中,不管t取何值,都有
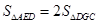 ;
;(2)当t取何值时,
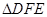 与
与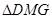 全等;
全等;(3)在(2)的前提下,若
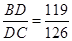 ,
,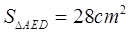 ,求
,求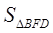 。
。(1)证明见解析;(2)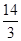 ;(3)
;(3)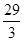 .
.
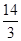 ;(3)
;(3)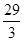 .
.试题分析:(1)由角平分线的性质可知DF=DM,所以△AED和△DEG的面积转化为底AE和CG的比值,根据路程=速度×时间求出AE和CG的长度即可证明在运动过程中,不管取何值,都有S△AED=2S△DGC.
(2)若△DFE与△DMG全等,则EF=MG,利用已知条件求出EF和MG的长度,建立方程解方程即可求出运动的时间.
(3)利用等高三角形的面积比等于对应底的比,即可求得答案.
试题解析:(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
∵S△AED=
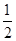 AE•DF,S△DGC=
AE•DF,S△DGC=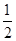 CG•DM,
CG•DM,∴
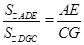 ,
,∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴AE=2tcm,CG=tcm,
∴
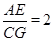 ,即
,即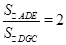 ,
,∴在运动过程中,不管取何值,都有S△AED=2S△DGC.
(2)解:设时间为t时,△DFE与△DMG全等,则EF=MG
①当M在线段CG的延长线上时,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴EF=AF-AE=10-2t,MG=AC-CG-AM=4-t,
即10-2t=4-t,
解得:t=6,
当t=6时,MG=-2,所以舍去;
②当M在线段CG上时,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴EF=AF-AE=10-2t(cm),MG=AM-(AC-CG)=t-4(cm),
即10-2t=t-4,
解得:t=
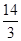 ,
,综上所述当t=
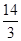 时,△DFE与△DMG全等.
时,△DFE与△DMG全等.(3)∵t=
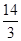 ,
,∴AE=2t=
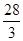 (cm),
(cm),∵DF=DM,
∴S△ABD:S△ACD=AB:AC=BD:CD=119:126,
∵AC=14cm,
∴AB=
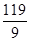 (cm),
(cm),∴BF=AB-AF=
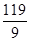 -10=
-10=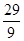 (cm),
(cm),∵S△ADE:S△BDF=AE:BF=
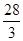 :
: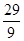 ,S△AED=28cm2,
,S△AED=28cm2,∴S△BDF=
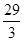 (cm2).
(cm2).考点: 1.全等三角形的判定与性质;2.三角形的面积;3.角平分线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目