Question

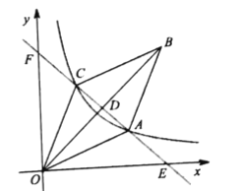
【题目】如图，在平面直角坐标系中，菱形的顶点在反比例函数图象上，直线交于点，交正半轴于点，且

求的长:

若，求的值．

Answer 1

【答案】（1）6；（2）4

【解析】

（1）首先利用勾股定理求出EF的长，然后结合题意利用菱形的性质证明出△DOE为等腰三角形，由此求出DO，最后进一步求解即可；

（2）过点A作AN⊥OE，垂足为E，在Rt△AON中，利用勾股定理求出AN的长，然后进一步根据反比例函数的性质求出值即可.

（1）∵，

∴EF=，∠OEF=∠OFE=45°，

∵四边形OABC为菱形，

∴OA=AB=BC=OC，OB⊥AC，DO=DB，

∴△DOE为等腰三角形，

∴DO=DE=EF=3，

∴OB=2DO=6；

（2）

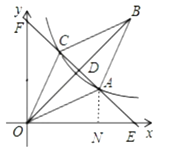
如图，过点A作AN⊥OE，垂足为E，则△ANE为等腰直角三角形，

∴AN=NE，

设AN=，则NE=，ON=，

在Rt△AON中，由勾股定理可得：，

解得：，，

当时，A点坐标为：(，)，C点坐标为：(，)；

当时，C点坐标为：(，)，A点坐标为：(，)；

∴.