��Ŀ����
����Ŀ���������ܻ��س����������Ի��ܣ�̫����6Ԫ/�裬����10Ԫ/�裮���ι����������20��ʱ������20�貿�ֵ����۸��8�ۣ�
��1�����̫�����ĸ�����![]() ��Ԫ�����ڹ�����
��Ԫ�����ڹ�����![]() ���裩�ĺ�����ϵʽ��
���裩�ĺ�����ϵʽ��
��2��������ĸ�����![]() ��Ԫ�����ڹ�����
��Ԫ�����ڹ�����![]() ���裩�ĺ�����ϵʽ��
���裩�ĺ�����ϵʽ��
��3��Ϊ��������������С���ƻ����û��ع��������ֻ��ܹ�90�裬����̫������������������������һ�룮���ֻ��ܸ��������ʱ���ܷ������٣����ٷ����Ƕ���Ԫ��
���𰸡���1����y1=6x����2��y2=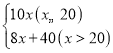 ����3��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ
����3��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ
��������
��1�������ܼ�=���������������̫�����ĸ�����y1��Ԫ�����ڹ�����x���裩�ĺ�������ʽ��
��2�������������һ�ι������������20�裻��һ�ι����������20�裻�����ܼ�=������������������ĸ�����y2��Ԫ�����ڹ�����x���裩�ĺ�������ʽ���ɣ�
��3������̫������������������������һ�룬�ɵ�̫�����������������ֻ�������![]() ����̫��������������30�裬������������������60�裻Ȼ����̫������������x�裬������������90-x�裬�����ܼ�=����������������������ֻ����ܷ����Ƕ��٣������жϳ����ֻ��ܸ��������ʱ���ܷ������٣����ٷ����Ƕ���Ԫ���ɣ�
����̫��������������30�裬������������������60�裻Ȼ����̫������������x�裬������������90-x�裬�����ܼ�=����������������������ֻ����ܷ����Ƕ��٣������жϳ����ֻ��ܸ��������ʱ���ܷ������٣����ٷ����Ƕ���Ԫ���ɣ�
�⣺��1��̫�����ĸ�����y1��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�y1=6x��
��2����һ�ι������������20��ʱ��
������y2��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�y2=10x��x��20����
��һ�ι����������20��ʱ��
������y2��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�
y2=10��20+10��0.8��(x-20)
=200+8x-160
=8x+40
���ϣ��ɵ�
���ĸ�����y2��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�
y2=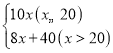
��3���������⣬�ɵ�̫����������������90��![]() ���裩��
���裩��
�����������������ڣ�90-30=60���裩��
��̫������������x�裬������������(90-x)�裬�������ֻ����ܷ�����yԪ��
��x��30��
��y=6x+[8(90-x)+40]
=6x+[760-8x]
=760-2x��
��-2��0��
��y��x�����������
��x��30��
�൱x=30ʱ��
y��С=760-2��30=700��Ԫ����
90-30=60�裬
��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��

����Ŀ����һ�������ĺ�����װ��ֻ����ɫ��ͬ�ĺڡ���������50����Сӱ������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣��±��������е�һ��ͳ�����ݣ�
������Ĵ��� | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ��� | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
��������ĸ��� | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
��1������Ƶ�![]() �ܴ�ʱ�����������Ƶ�ʽ���ӽ�______������ȷ��0.1����
�ܴ�ʱ�����������Ƶ�ʽ���ӽ�______������ȷ��0.1����
��2�����������һ�Σ���������ĸ���P��������______��
��3���Թ���������ɫ�����ж��ٸ���