题目内容
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
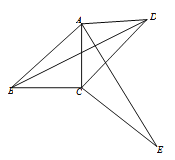
(1)求证:AE⊥BD;
(2)若AD=2,CD=3,试求四边形ABCD的对角线BD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由旋转的性质可得AC=BC,∠DBC=∠CAE,即可得∠ACB=90°,根据直角三角形的性质可得AE⊥BD,
(2)由旋转的性质可得CD=CE=3,BD=AE,∠DCE=∠ACB=90°,由勾股定理可求BD的长.
(1)如图,设AC与BD的交点为点M,BD与AE的交点为点N,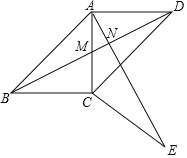
∵旋转
∴AC=BC,∠DBC=∠CAE
又∵∠ABC=45°,
∴∠ABC=∠BAC=45°,
∴∠ACB=90°,
∵∠DBC+∠BMC=90°
∴∠AMN+∠CAE=90°
∴∠AND=90°
∴AE⊥BD,
(2)如图,连接DE,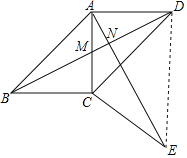
∵旋转
∴CD=CE=3,BD=AE,∠DCE=∠ACB=90°
∴DE=![]() =3
=3![]() ,∠CDE=45°
,∠CDE=45°
∵∠ADC=45°
∴∠ADE=90°
∴EA=![]() =
=![]()
∴BD=![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目