题目内容
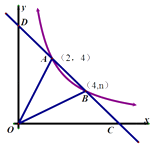
【题目】如图,直线y=ax+b与反比例函数 ![]() (x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点.
(x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点.
(1)求m,n的值;
(2)求△AOB的面积;
(3)若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.
【答案】
(1)解:将A(2,4)代入 ![]() 中得m=8,再代入B(4,n)中得n=2
中得m=8,再代入B(4,n)中得n=2
(2)解:∵直线y=ax+b经过点A(2,4),B(4,2),
∴ ![]() ,
,
解得a=﹣1,b=6.∴y=﹣x+6,
C,D坐标为:C(6,0),D(0,6)
S△AOB=S△COD﹣S△AOD﹣S△COB= ![]() ×6×6﹣
×6×6﹣ ![]() ×6×2﹣
×6×2﹣ ![]() ×6×2=18﹣6﹣6=6
×6×2=18﹣6﹣6=6
(3)解:当x=y时,x=﹣x+6,解得x=3,所以,P点坐标为(3,3).
【解析】(1)将A(2,4)代入 y=![]() 中可求得得m,再代入B(4,n)即可求得n;
中可求得得m,再代入B(4,n)即可求得n;
(2)由待定系数法求出直线y=ax+b的解析式,进而求得与坐标轴的交点,再由C,D坐标和S△AOB=S△COD-S△AOD-S△COB代入即可;
(3)把x=y代入y=-x+6,可求得x的值,进而求得P点纵坐标。
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.

练习册系列答案
相关题目
【题目】红星中学计划组织“春季研修活动,活动组织负责人从公交公司了解到如下租车信息:
车型 |
|
|
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
校方从实际情况出发,决定租用![]() 、
、![]() 型客车共
型客车共![]() 辆,而且租车费用不超过
辆,而且租车费用不超过![]() 元。
元。
(1)请为校方设计可能的租车方案;
(2)在(1)的条件下,校方根据自愿的原则,统计发现有![]() 人参加,请问校方应如何租车,且又省钱?
人参加,请问校方应如何租车,且又省钱?