题目内容
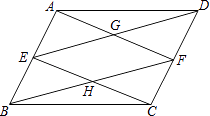
【题目】如图,CD AB ,EF AB ,垂足分别为 D、F,1 2 ,若A 65 ,B 45 , 求AGD 的度数.

【答案】AGD 70°.
【解析】
由CD⊥AB,EF⊥AB可得出∠CDF=∠EFB=90°,利用“同位角相等,两直线平行”可得出CD∥EF,利用“两直线平行,同位角相等”可得出∠DCB=∠1,结合∠1=∠2可得出∠DCB=∠2,利用“内错角相等,两直线平行”可得出DG∥BC,利用“两直线平行,同位角相等”可得出∠ADG的度数,在△ADG中,利用三角形内角和定理即可求出∠AGD的度数.
∵CD⊥AB,EF⊥AB
∴CDF=EFB=90 °
∴CD∥EF
∴DCB=1
∵1=2
∴DCB=2
∴ DG∥BC
∴ADG=B=45 °
又∵在△ADG中,A=65 °,ADG=45 °
∴AGD=180-A-ADG=70°.

 字词句段篇系列答案
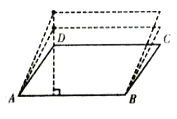
字词句段篇系列答案【题目】如图,在平行四边形![]() 中,当底边
中,当底边![]() 上的高
上的高![]() 由小到大变化时,平行四边形
由小到大变化时,平行四边形![]() 的面积
的面积![]() 也随之发生变化,我们得到如下数据:
也随之发生变化,我们得到如下数据:
底边AB上的高x(cm) | 2 | 3 | 4 | 5 |
平行四边形ABCD的面积y(cm2) | 12 | 18 | 24 | 30 |
(1)在这个变化过程中,自变量、因变量分别是什么?
(2)![]() 与
与![]() 之间的关系式可以表示为 ;
之间的关系式可以表示为 ;
(3)由表格中的数据可以发现,当![]() 每增加
每增加![]() 时,
时,![]() 如何变化?
如何变化?
(4)若平行四边形![]() 的面积为
的面积为![]() ,此时底边
,此时底边![]() 上的高为多少?
上的高为多少?
【题目】八(3)班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图(如图)
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有3000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?