题目内容
【题目】在四边形ABCD中，∠B=90°，AC=4，AB∥CD，DH垂直平分AC，点H为垂足，设AB=x，AD=y，则y关于x的函数关系用图象大致可以表示为（ ）
A.
B.
C.
D.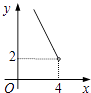
【答案】C
【解析】解：∵DH垂直平分AC，
∴AD=CD=y，AH=CH= 
AC=2，∠CHD=90°，
∵CD∥AB，
∴∠DCH=∠BAC，
∴△CDH∽△ACB，
∴ 
= 
， 
= 
，
∴y= 
（0＜x＜4）．
所以答案是：C．
【考点精析】通过灵活运用线段垂直平分线的性质和相似三角形的判定与性质，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．
练习册系列答案
相关题目
【题目】八（3）班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班50名学生的处理方式进行统计，得出相关统计表和统计图（如图）
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题：
（1）统计表中的m= ，n= ；
（2）补全频数分布直方图；
（3）若该校有3000名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？
