题目内容
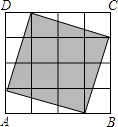
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )

A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
【答案】B
【解析】
表示出左上角与右下角部分的面积,求出之差,根据差与BC无关即可求出a与b的关系式.
如图,设左上角阴影部分的长为AE,宽为AF=3b,
右下角阴影部分的长为PC,宽为CG=a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差![]() .
.
∵S始终保持不变,∴3b﹣a=0,即a=3b.
故选B.


练习册系列答案
相关题目
【题目】为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
部分时段车流量情况调查表
时间 | 负责组别 | 车流总量 | 每分钟车流量 |
早晨上学6:30~7:00 | ①② | 2747 | 92 |
中午放学11:20~11:50 | ③④ | 1449 | 48 |
下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
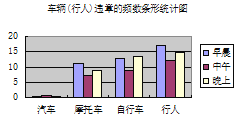
回答下列问题:
(1)请你写出2条交通法规.
(2)早晨.中午.晚上三个时段每分钟车流量的极差是多少,这三个时段的车流总量的中位数是多少.
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(4)通过分析写一条合理化建议.