Question

如图，正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN⊥DM，且交∠CBE的平分线于点N． (1)求证：MD＝MN． (2)若将上述条件中的“M是AB的中点”改为“M是AB上的任一点”，其他条件不变，则结论“MD＝MN”还成立吗？若成立，请证明；若不成立，请说明理由．

Answer 1

答案：
解析：

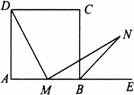
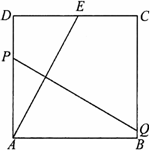
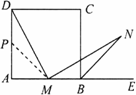
(1)证明：取AD的中点P，连接PM，则． 　　∵四边形ABCD是正方形， 　　∴AD＝AB，∠A＝∠ABC＝90°， 　　∴∠PDM＋∠AMD＝90°， 　　∵DM⊥MN， 　　∴∠NMB＋∠AMD＝90°， 　　∴∠PDM＝∠BMN． 　　∵M为AB的中点， 　　∴， 　　∴DP＝MB，AP＝AM， 　　∴∠APM＝∠AMP＝45°，∴∠DPM＝135°． 　　∵BN平分∠CBE，∴∠CBN＝45°， 　　∴∠MBN＝∠MBC＋∠CBN＝90°＋45°＝135°． 　　即∠DPM＝∠MBN， 　　∴△DPM≌△MBN，∴DM＝MN． 　　(2)解：结论仍然成立． 　　证明：在AD上截取AP＝MA，连接MP，则DP＝AD－AP， 　　BM＝AB－AM，∴DP＝MB． 　　同(1)可证， 　　∠PDM＝∠BMN，∠DPM＝∠MBN＝135°， 　　∴△DPM≌△MBN， 　　∴DM＝MN．