题目内容
已知:如图,□ABCD中,∠ABC的平分线交AD于E,
∠CDA的平分线交BC于F.

(1)求证:△ABE≌△CDF;(2)连接EF、BD,求证:EF与BD互相平分.
∠CDA的平分线交BC于F.

(1)求证:△ABE≌△CDF;(2)连接EF、BD,求证:EF与BD互相平分.
(1)通过角边角证明△ABE≌△CDF;(2)证明四边形BFDE是平行四边形∴EF与BD互相平分.
试题分析:(1)证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD;
∠A=∠C,∠ABC=∠CDA.
∵BE平分∠ABC,DF平分∠CDA,
∴∠ABE=
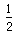 ∠ABC,∠CDF=
∠ABC,∠CDF=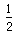 ∠CDA.
∠CDA.∴∠ABE=∠CDF.
∴△ABE≌△CDF.
(2)证明:∵△ABE≌△CDF,
∴AE=CF 又AD=BC.
∴DE=BF且DE∥BF.
∴四边形BFDE是平行四边形.
∴EF与BD互相平分.
点评:本题考查全等三角形的证明及平行四边形的判断,解决此题须考生熟悉全等三角形的证明及平行四边形的判断方法,此类题是中考的重点

练习册系列答案
相关题目
 的位置如图所示,点
的位置如图所示,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ;延长
;延长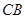 交
交 轴于点
轴于点 ,作正方形
,作正方形 ;延长
;延长 交
交 ,作正方形
,作正方形 …;按这样的规律进行下去,第
…;按这样的规律进行下去,第 个正方形的面积为
个正方形的面积为



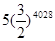
 ,
, ,
, ,
, ,直线
,直线 将四边形
将四边形 分成面积相等的两部分,则
分成面积相等的两部分,则 的值为 .
的值为 . 边形的内角和为1260°,则
边形的内角和为1260°,则
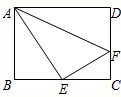
 BFD.
BFD.
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想. 
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的延长线于
的延长线于 ,且
,且 ,连接
,连接 .
.
 ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.