Question

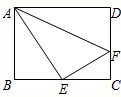
如图，在矩形ABCD中，AB=9，BC=12，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，则DF的长为（    ）

A．4

B．6

C．8

D．9

Answer 1

B

试题分析：

作点E关于直线CD的对称点E′，连接AE′交CD于点F
AE的长度是固定的，要△AEF的周长最小，只要AF+EF最小即可，又根据三角形两边之和大于第三边可知，对CD上任意点F′,总有AF′+E′F′＞AE′,所以点F是使得AF+EF最小的点。。
∵在矩形ABCD中，AB=9，BC=12，点E是BC中点，
∴BE=CE=CE′=6，
∵AB⊥BC，CD⊥BC，
∴△CE′F∽△BE′A，即CE′·AB=CF·BE′，即6×9=CF·(12+6)，解得CF=3，
∴DF=CD-CF=9-3=6
故选B
点评：难度中等，动点问题，关键在于理解要△AEF的周长最小，只要AF+EF最小。