��Ŀ����
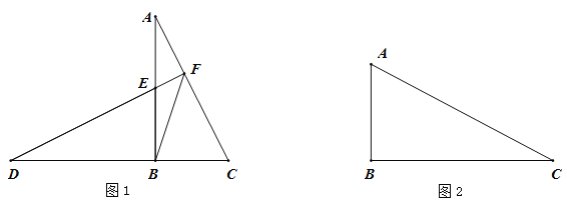
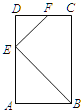
����Ŀ��ijũ��Ҫ��һ����������������![]() ����������һ�濿ǽ��ǽ�����ó���Ϊ27�ף�����������ľ��Χ�ɣ��м�Ҳ��ľ���������ֳ��������أ�������ͼ��ʾ����������1�����ţ�����ľ���������ɺ�ľ���ܳ�60�ף�����������������
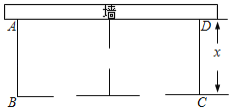
����������һ�濿ǽ��ǽ�����ó���Ϊ27�ף�����������ľ��Χ�ɣ��м�Ҳ��ľ���������ֳ��������أ�������ͼ��ʾ����������1�����ţ�����ľ���������ɺ�ľ���ܳ�60�ף�����������������![]() �Ŀ�Ϊ
�Ŀ�Ϊ![]() �ף�
�ף�
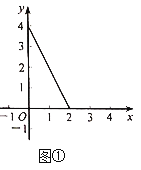
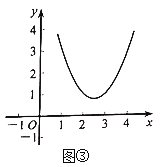
��1�����������ij�![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���������������Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��3����![]() Ϊ��ֵʱ����������������ʱ�������ﵽ��������Ϊ����
Ϊ��ֵʱ����������������ʱ�������ﵽ��������Ϊ����![]() ��
��
���𰸡���1��![]() �ף���2��15����3����
�ף���2��15����3����![]() Ϊ12ʱ����������������������Ϊ
Ϊ12ʱ����������������������Ϊ![]() ��
��
��������
��1�����������ͼ�Σ������ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() �ij���
�ij���
��2�����ݳ����ε�������㹫ʽ���Եõ���Ӧ�ķ��̣��Ӷ����Եõ�![]() ��ֵ��ע��ǽ�����ó���Ϊ27�ף�
��ֵ��ע��ǽ�����ó���Ϊ27�ף�
��3������������Եõ�![]() ��
��![]() �ĺ�����ϵʽ��Ȼ����ݶ��κ��������ʺ�
�ĺ�����ϵʽ��Ȼ����ݶ��κ��������ʺ�![]() ��ȡֵ��Χ����ɣ�
��ȡֵ��Χ����ɣ�
�⣺��1����ͼ�ɵã�![]() �ij���
�ij���![]() ����
����![]() ��
��
��![]() �ij���
�ij���![]() �ף�
�ף�
��2����![]() ����ã�
����ã�![]() ��
��![]() ��
��
![]() ����
����![]() ��
��![]() ��
��
��![]() ��ֵ��15��
��ֵ��15��
��3�����������������![]() ����
����![]() ��
��
![]() ����
����![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ȡ�����ֵ����ʱ
ȡ�����ֵ����ʱ![]() ��
��
�𣺵�![]() Ϊ12ʱ����������������ʱ�������ﵽ��������Ϊ
Ϊ12ʱ����������������ʱ�������ﵽ��������Ϊ![]() ��
��

 ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�����Ŀ���ס�����λͬѧ5����ѧѡ�����ijɼ�ͳ�����±�������5�ο��Ե��ܳɼ���ͬ����ͬѧ������������⣺
��1 �� | ��2 �� | �� 3�� | �� 4�� | ��5 �� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 |
| 70 |
��1��ͳ�Ʊ��У���![]() ��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��2��Сӱ�����˼�ͬѧ�ijɼ�ƽ����Ϊ60��������![]() [(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
[(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
���������ͬѧ�ɼ���ƽ�����ͷ��
��3����ƽ�����ͷ���ĽǶȷ�����������λͬѧ˭�ijɼ����ȶ�.