题目内容
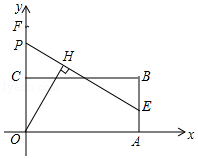
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0，②当﹣1≤x≤3时，y＜0；③3a+c=0；④若（x1 ， y1）（x2、y2）在函数图象上，当0＜x1＜x2时，y1＜y2 ， 其中正确的是（ ）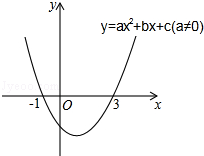 
A.①②④
B.①③
C.①②③
D.①③④
【答案】B
【解析】解：∵函数图象的对称轴为：x=﹣ 
= 
=1， ∴b=﹣2a，即2a+b=0，①正确；
由图象可知，当﹣1＜x＜3时，y＜0，②错误；
由图象可知，当x=1时，y=0，
∴a﹣b+c=0，
∵b=﹣2a，
∴3a+c=0，③正确；
∵抛物线的对称轴为x=1，开口方向向上，
∴若（x1 ， y1）、（x2 ， y2）在函数图象上，当1＜x1＜x2时，y1＜y2；当x1＜x2＜1时，y1＞y2；
故④错误；
故选：B．
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案，需要熟知二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
【题目】某公司以每吨
元的价格收购了
吨某种药材，若直接在市场上销售，每吨的售价是
元．该公司决定加工后再出售，相关信息如下表所示：
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 （元/吨） |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材；②加工后的废品不产生效益.)
受市场影响，该公司必须在
天内将这批药材加工完毕．
（1）若全部粗加工，可获利_______________________元；
（2）若尽可能多的精加工，剩余的直接在市场上销售，可获利_____________元；
（3）若部分粗加工，部分精加工，恰好天完成，求可获利多少元?
