题目内容
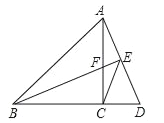
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
【答案】(1)证明见解析;(2)45°;(3)BE=AE+![]() CE.
CE.
【解析】
试题(1)由垂直的定义得到∠ACB=90°根据全等三角形的判定定理即可得到结论;
(2)取AB的中点M,连接CM,EM,根据圆周角定理即可得到结论;
(3)作CG⊥CE交BE于G,根据等腰直角三角形的性质得到CG=CE,根据全等三角形的性质得到BG=AE,于是得到结论.
试题解析:解:(1)∵BE⊥AD,∠ACB=90°,∴∠1=∠2=90°﹣∠D,在△BCF和△ACD中,∵∠1=∠2,BC=AC,∠BCF=∠ACD=90°,∴△BCF≌△ACD;
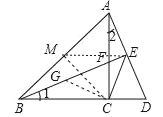
(2)∠BEC=45°.理由:取AB的中点M,连接CM,EM,则CM=EM=![]() AB=AM=BM,∴点A,B,C,E在同一个圆(⊙M)上,∴∠BEC=∠BAC=45°;
AB=AM=BM,∴点A,B,C,E在同一个圆(⊙M)上,∴∠BEC=∠BAC=45°;
(3)BE=AE+![]() CE.证明如下:
CE.证明如下:
作CG⊥CE交BE于G,∵∠BEC=45°,则∠CGE=45°=∠BEC,CG=CE,∴∠BGC=135°=∠AEC,EG=![]() CE,在△BCG和△ACE中,∵∠1=∠2,∠BGC=∠AEC,BC=AC,∴△BCG≌△ACE,∴BG=AE,∴BE=BG+EG=AE+
CE,在△BCG和△ACE中,∵∠1=∠2,∠BGC=∠AEC,BC=AC,∴△BCG≌△ACE,∴BG=AE,∴BE=BG+EG=AE+![]() CE.
CE.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目







