ЬтФПФкШн
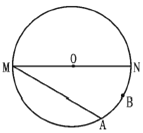
ЁОЬтФПЁПЖЈвхЃКгаСНЬѕБпГЄЕФБШжЕЮЊ![]() ЕФжБНЧШ§НЧаЮНазіЁАїШСІШ§НЧаЮЁБЮвУЧжЊЕРЃЌУќЬтЁАжБНЧШ§НЧаЮ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЁБЪЧвЛИіецУќЬтЃЌЫљвдЁАКЌ30ЁуНЧЕФжБНЧШ§НЧаЮЁБОЭЪЧвЛИіЁАїШСІШ§НЧаЮЁБ
ЕФжБНЧШ§НЧаЮНазіЁАїШСІШ§НЧаЮЁБЮвУЧжЊЕРЃЌУќЬтЁАжБНЧШ§НЧаЮ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЁБЪЧвЛИіецУќЬтЃЌЫљвдЁАКЌ30ЁуНЧЕФжБНЧШ§НЧаЮЁБОЭЪЧвЛИіЁАїШСІШ§НЧаЮЁБ
ЃЈ1ЃЉЩшЁАїШСІШ§НЧаЮЁБНЯЖЬжБНЧБпЮЊaЃЌНЯГЄжБНЧБпЮЊbЃЌЧыФужБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
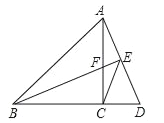
ЃЈ2ЃЉШчЭМЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌBCЃН6ЃЌDЪЧABЕФжаЕуЃЌЕуEдкCDЩЯЃЌТњзуADЃНDEЃЌСЌНсAEЃЌЙ§ЕуDзїDFЁЮAEНЛBCгкЕуF
ЂйШчЙћЕуEЪЧCDЕФжаЕуЃЌЧѓжЄЃКЁїBDFЪЧЁАїШСІШ§НЧаЮЁБ
ЂкШчЙћЁїBDFЪЧЁАїШСІШ§НЧаЮЁБЃЌЧвBFЃН![]() BCЃЌЧѓЯпЖЮACЕФГЄ
BCЃЌЧѓЯпЖЮACЕФГЄ
ЃЈЖўДЮИљЪНдЫЫуЬсЪОЃКЃЈ![]() ЃЉ2ЃНn2ЃЈ
ЃЉ2ЃНn2ЃЈ![]() ЃЉ2ЃНn2aЃЌБШШчЃКЃЈ4
ЃЉ2ЃНn2aЃЌБШШчЃКЃЈ4![]() ЃЉ2ЃН42
ЃЉ2ЃН42![]() ЃЈ
ЃЈ![]() ЃЉ2ЃН16ЁС3ЃН48ЃЉ
ЃЉ2ЃН16ЁС3ЃН48ЃЉ

ЁОД№АИЁПЃЈ1ЃЉ![]() Лђ2;ЃЈ2ЃЉЂйМћНтЮі;ЂкACЕФГЄЮЊ2
Лђ2;ЃЈ2ЃЉЂйМћНтЮі;ЂкACЕФГЄЮЊ2![]() Лђ10Лђ2
Лђ10Лђ2![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшаББпГЄЮЊcЃЌЗжСНжжЧщПіЂйЕБ![]() ЪБЃЌc=2aЃЌгЩЙДЙЩЖЈРэЧѓГіbЃЌМДПЩЕУГі
ЪБЃЌc=2aЃЌгЩЙДЙЩЖЈРэЧѓГіbЃЌМДПЩЕУГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЕБ![]() ЪБЃЌb=2aЃЌМДПЩЕУГі
ЪБЃЌb=2aЃЌМДПЩЕУГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЂйжЄГіЁЯBCD=30ЁуЃЌЕУГіЁЯBDC=60ЁуЃЌгЩЦНааЯпЕФаджЪКЭЕШбќШ§НЧаЮЕФаджЪЕУГіЁЯEDF=ЁЯBDF=30ЁуЃЌгЩжБНЧШ§НЧаЮЕФаджЪЕУГіBF=![]() DFЃЌМДПЩЕУГіНсТлЃЛ
DFЃЌМДПЩЕУГіНсТлЃЛ
ЂкЗжЫФжжЧщПі ЕБ![]() =
=![]() ЪБЃЌЧѓГіBD=
ЪБЃЌЧѓГіBD=![]() BF=1ЃЌЕУГіAB=2BD=2ЃЌгЩЙДЙЩЖЈРэЕУГіAC=
BF=1ЃЌЕУГіAB=2BD=2ЃЌгЩЙДЙЩЖЈРэЕУГіAC=![]() =2
=2![]() ЃЛ
ЃЛ
ЕБ![]() =
=![]() ЪБЃЌЧѓГіBD=2BF=4ЃЌЕУГіAB=2BD=8ЃЌгЩЙДЙЩЖЈРэAC=
ЪБЃЌЧѓГіBD=2BF=4ЃЌЕУГіAB=2BD=8ЃЌгЩЙДЙЩЖЈРэAC=![]() =10ЃЛ
=10ЃЛ
ЕБ![]() =
=![]() ЪБЃЌЧѓГіDF=2BF=4ЃЌгЩЙДЙЩЖЈРэЕУГіBD=
ЪБЃЌЧѓГіDF=2BF=4ЃЌгЩЙДЙЩЖЈРэЕУГіBD=![]() =2
=2![]() ЃЌЕУГіAB=2BD=4
ЃЌЕУГіAB=2BD=4![]() ЃЌгЩЙДЙЩЖЈРэЕУГіAC=
ЃЌгЩЙДЙЩЖЈРэЕУГіAC=![]() =2
=2![]() ЃЛ
ЃЛ
ЕБ![]() =
=![]() ЪБЃЌгЩЙДЙЩЖЈРэЧѓГіBD=
ЪБЃЌгЩЙДЙЩЖЈРэЧѓГіBD=![]() ЃЌЕУГіAB=2BD=
ЃЌЕУГіAB=2BD=![]() ЃЌгЩЙДЙЩЖЈРэЕУГіAC=
ЃЌгЩЙДЙЩЖЈРэЕУГіAC=![]() =
=![]() МДПЩЃЎ
МДПЩЃЎ
ЃЈ1ЃЉНтЃКЩшаББпГЄЮЊcЃЌЗжСНжжЧщПіЃК
ЂйЕБ![]() ЪБЃЌcЃН2aЃЌ
ЪБЃЌcЃН2aЃЌ
дђbЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌbЃН2aЃЌ
ЪБЃЌbЃН2aЃЌ
Ёр![]() ЃН2ЃЛ
ЃН2ЃЛ
злЩЯЫљЪіЃЌ![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() Лђ2ЃЛ
Лђ2ЃЛ
ЃЈ2ЃЉЂйжЄУїЃКЁпDЪЧABЕФжаЕуЃЌ
ЁрADЃНBDЃЌ
ЁпADЃНDEЃЌ
ЁрBDЃНDEЃЌ
ЁпЕуEЪЧCDЕФжаЕуЃЌ
ЁрDEЃН![]() CDЃЌ
CDЃЌ
ЁрBDЃН![]() CDЃЌ
CDЃЌ
ЁпЁЯBЃН90ЁуЃЌ
ЁрЁЯBCDЃН30ЁуЃЌ
ЁрЁЯBDCЃН60ЁуЃЌ
ЁпDFЁЮAEЃЌ
ЁрЁЯDEAЃНЁЯEDFЃЌЁЯDAEЃНЁЯBDFЃЌ
ЁпADЃНDEЃЌ
ЁрЁЯDAEЃНЁЯDEAЃЌ
ЁрЁЯEDFЃНЁЯBDFЃН30ЁуЃЌ
ЁрBFЃН![]() DFЃЌ
DFЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЁїBDFЪЧЁАїШСІШ§НЧаЮЁБЃЛ
ЂкНтЃКЗжЫФжжЧщПіЃК
ЕБ![]() =
=![]() ЪБЃЌ
ЪБЃЌ
ЁпBFЃН![]() BCЃЌBCЃН6ЃЌ
BCЃЌBCЃН6ЃЌ
ЁрBFЃН2ЃЌ
ЁрBDЃН![]() BFЃН1ЃЌ
BFЃН1ЃЌ
ЁпDЪЧABЕФжаЕуЃЌ
ЁрABЃН2BDЃН2ЃЌ
ЁрACЃН![]() ЃН
ЃН![]() ЃН2
ЃН2![]() ЃЛ
ЃЛ
ЕБ![]() =
=![]() ЪБЃЌ
ЪБЃЌ
ЁпBFЃН![]() BCЃЌBCЃН6ЃЌ
BCЃЌBCЃН6ЃЌ
ЁрBFЃН2ЃЌ
ЁрBDЃН2BFЃН4ЃЌ
ЁпDЪЧABЕФжаЕуЃЌ
ЁрABЃН2BDЃН8ЃЌ
ЁрACЃН![]() ЃН
ЃН![]() ЃН10ЃЛ
ЃН10ЃЛ
ЕБ![]() =
=![]() ЪБЃЌ
ЪБЃЌ
ЁпBFЃН![]() BCЃЌBCЃН6ЃЌ
BCЃЌBCЃН6ЃЌ
ЁрBFЃН2ЃЌ
ЁрDFЃН2BFЃН4ЃЌ
ЁрBD=![]() =
=![]() =2
=2![]() ЃЌ
ЃЌ
ЁпDЪЧABЕФжаЕуЃЌ
ЁрABЃН2BDЃН4![]() ЃЌ
ЃЌ
ЁрAC=![]() =2
=2![]() ЃЛ
ЃЛ
ЕБ![]() =
=![]() ЪБЃЌ
ЪБЃЌ
ЁрDFЃН2BDЃЌ
ЁпBFЃН![]() BCЃЌBCЃН6ЃЌ
BCЃЌBCЃН6ЃЌ
ЁрBFЃН2ЃЌ
гЩЙДЙЩЖЈРэЕУЃКDF2ЉBD2ЃНBF2ЃЌМДЃЈ2BDЃЉ2ЉBD2ЃН22ЃЌ
НтЕУЃКBD=![]() ЃЌ
ЃЌ
ЁрABЃН2BDЃН![]() ЃЌ
ЃЌ
ЁрACЃН![]()
ЃН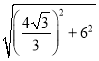 ЃН
ЃН![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌШчЙћЁїBDFЪЧЁАїШСІШ§НЧаЮЁБЃЌЧвBFЃН![]() BCЃЌЯпЖЮACЕФГЄЮЊ2
BCЃЌЯпЖЮACЕФГЄЮЊ2![]() Лђ10Лђ2
Лђ10Лђ2![]() Лђ
Лђ![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПББОЉЪРНчдАвеВЉРРЛсЃЈМђГЦЁАЪРдАЛсЁБЃЉдАЧј2019Фъ4дТ29ШежС2019Фъ10дТ7ШедкжаЙњББОЉЪабгЧьЧјОйааЃЌУХЦБМлИёШчБэЃКаЁУїШЋМвгк9дТ28ШеМЏЬхШыдАВЮЙлгЮРРЃЌЭЈЙ§МЦЫуЗЂЯжЃКШєЬсЧАСНЬьЯпЩЯЙКТђУХЦБЫљашЗбгУЮЊ996дЊЃЌЖјШыдАЕБЬьЙКЦБЫљашЗбгУЮЊ1080дЊЃЌдђИУМвЭЅжаПЩвдЙКТђгХЛнЦБЕФга_____ШЫЃЎ
ЦБжж | ЦБМлЃЈдЊ/ШЫЃЉ | |
жИЖЈШе | ЦеЭЈЦБ | 160 |
гХЛнЦБ | 100 | |
ЦНШе | ЦеЭЈЦБ | 120 |
гХЛнЦБ | 80 | |
зЂ1ЃКЁАжИЖЈШеЁБЮЊПЊдАШеЃЈ4дТ29ШеЃЉЁЂЮхвЛРЭЖЏНкЃЈ5дТ1ШеЃЉЁЂЖЫЮчНкЁЂжаЧяНкЁЂЪЎвЛМйЦкЃЈКЌБедАШеЃЉЃЌЁАЦНШеЁБЮЊЪРдАЛсЛсЦкГ§ЁАжИЖЈШеЁБЭтЕФЦфЫћШеЦкЃЛ
зЂ2ЃКСљЪЎжмЫъМАвдЩЯРЯШЫЁЂЪЎАЫжмЫъвдЯТЕФбЇЩњОљПЩЙКТђгХЛнЦБЃЛ
зЂ3ЃКЬсЧАСНЬьМАвдЩЯЯпЩЯЙКТђЪРдАЛсУХЦБЃЌЦБМлПЩДђОХелЃЌЕЋНіЯогкЦеЭЈЦБЃЎ