题目内容
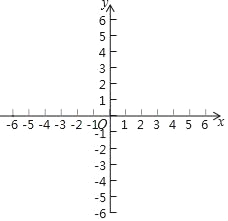
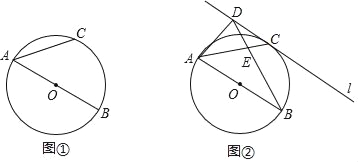
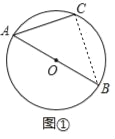
【题目】如图①,AB是⊙O的直径,![]() ,连接AC.
,连接AC.
(1)求证:∠CAB=45°;
(2)如图②,直线l经过点C,在直线l上取一点D,使BD=AB,BD与AC相交于点E,连接AD,且AD=AE.
①求证:直线l是⊙O的切线;
②求![]() 的值.
的值.
【答案】(1)证明见解析(2)①证明见解析②![]()
【解析】
(1)连接BC,由![]() 知∠CAB=∠ABC,根据AB为⊙O的直径得∠ACB=90°,据此可得答案;(2)①连接OC、作DP⊥AB,设∠ABD=α,先根据AD=AE、BA=BD求得∠ABD=∠DAE=30°,据此知PD=
知∠CAB=∠ABC,根据AB为⊙O的直径得∠ACB=90°,据此可得答案;(2)①连接OC、作DP⊥AB,设∠ABD=α,先根据AD=AE、BA=BD求得∠ABD=∠DAE=30°,据此知PD=![]() BD=
BD=![]() AB,结合OC=
AB,结合OC=![]() AB知DP=OC,据此证得四边形DPOC为矩形,继而得证;②证△ACD∽△BAE得
AB知DP=OC,据此证得四边形DPOC为矩形,继而得证;②证△ACD∽△BAE得![]() =
=![]() =
=![]() ,据此知AE=
,据此知AE=![]() CD,作EI⊥AB于点I,由∠CAB=45°、∠ABD=30°知BE=2EI=2×
CD,作EI⊥AB于点I,由∠CAB=45°、∠ABD=30°知BE=2EI=2×![]() AE=
AE=![]() AE=2CD,据此可得答案.
AE=2CD,据此可得答案.
(1)如图①,连接BC,
∵![]() ,
,
∴∠CAB=∠ABC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB=∠CBA=45°;
(2)①如图②,连接OC、作DP⊥AB于点P,
设∠ABD=α,
∵BA=BD,
∴∠BAD=∠BDA,
∵AD=AE,
∴∠ADE=∠AED,
∴∠AED=∠BAD,
∴∠DAE=∠DBA=α,
∵∠CAB=45°,
∴∠ADE=∠AED=∠CAB+∠ABD=45°+α,
∵∠DAE+∠ADE+∠AED=180°,
∴α+α+45°+α+45°=180°,
解得:α=30°,即∠ABD=∠DAE=30°,
在Rt△BPD中,PD=![]() BD=
BD=![]() AB,
AB,
又∵OC=![]() AB,
AB,
∴OC=PD,
∵△ABC是等腰直角三角形,OA=OB,
∴CO⊥AB,
∵DP⊥AB、CO⊥AB,
∴四边形DPOC是矩形,
∴∠OCD=90°,
∴直线l是⊙O的切线;
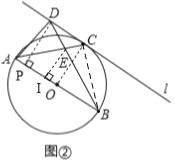
②由①知,∠CAD=∠ABE=30°,CD∥AB,
∴∠ACD=∠EAB=45°,
则△ACD∽△BAE,
∴![]() =
=![]() =
=![]() ,
,
∴AE=![]() CD,
CD,
如图②,作EI⊥AB于点I,
∵∠CAB=45°、∠ABD=30°,
∴BE=2EI=2×![]() AE=
AE=![]() AE=
AE=![]() ×
×![]() CD=2CD,
CD=2CD,
∴![]() =
=![]() .
.