题目内容
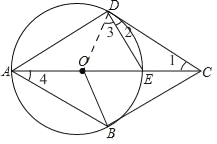
【题目】已知，四边形ABCD中，E是对角线AC上一点，DE＝EC，以AE为直径的⊙O与边CD相切于点D，点B在⊙O上，连接OB．
（1）求证：DE＝OE；
（2）若CD∥AB，求证：BC是⊙O的切线；
（3）在（2）的条件下，求证：四边形ABCD是菱形．
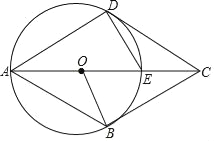
【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.
【解析】
（1）先判断出∠2+∠3＝90°，再判断出∠1＝∠2即可得出结论；
（2）根据等腰三角形的性质得到∠3＝∠COD＝∠DEO＝60°，根据平行线的性质得到∠4＝∠1，根据全等三角形的性质得到∠CBO＝∠CDO＝90°，于是得到结论；
（3）先判断出△ABO≌△CDE得出AB＝CD，即可判断出四边形ABCD是平行四边形，最后判断出CD＝AD即可．
（1）如图，连接OD，
∵CD是⊙O的切线，
∴OD⊥CD，
∴∠2+∠3＝∠1+∠COD＝90°，
∵DE＝EC，
∴∠1＝∠2，
∴∠3＝∠COD，
∴DE＝OE；
（2）∵OD＝OE，
∴OD＝DE＝OE，
∴∠3＝∠COD＝∠DEO＝60°，
∴∠2＝∠1＝30°，
∵AB∥CD，
∴∠4＝∠1，
∴∠1＝∠2＝∠4＝∠OBA＝30°，
∴∠BOC＝∠DOC＝60°，
在△CDO与△CBO中，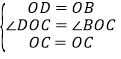
，
∴△CDO≌△CBO（SAS），
∴∠CBO＝∠CDO＝90°，
∴OB⊥BC，
∴BC是⊙O的切线；
（3）∵OA＝OB＝OE，OE＝DE＝EC，
∴OA＝OB＝DE＝EC，
∵AB∥CD，
∴∠4＝∠1，
∴∠1＝∠2＝∠4＝∠OBA＝30°，
∴△ABO≌△CDE（AAS），
∴AB＝CD，
∴四边形ABCD是平行四边形，
∴∠DAE＝
∠DOE＝30°，
∴∠1＝∠DAE，
∴CD＝AD，
∴ABCD是菱形．
【题目】温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元．设每天安排x人生产乙产品．
（1）根据信息填表
产品种类 | 每天工人数（人） | 每天产量（件） | 每件产品可获利润（元） |
甲 | 15 | ||
乙 |
|
|
（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．
（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值．
【题目】某地特产槟榔芋深受欢迎，某商场以7元/千克收购了3 000千克优质槟榔芋，若现在马上出售，每千克可获得利润3元．根据市场调查发现，近段时间内槟榔芋的售价每天上涨0.2元/千克，为了获得更大利润，商家决定先贮藏一段时间后再出售．根据以往经验，这批槟榔芋的贮藏时间不宜超过100天，在贮藏过程中平均每天损耗约10千克．
（1）若商家将这批槟榔芋贮藏x天后一次性出售，请完成下列表格：
每千克槟榔芋售价 （单位：元） | 可供出售的槟榔芋重量 （单位：千克） | |
现在出售 | 3 000 | |
x天后出售 |
（2）将这批槟榔芋贮藏多少天后一次性出售最终可获得总利润29 000元？
